[Algorithm] [Interview Question] Move Zeroes To End Of Array

To see the youtube video where I draw out how each algorithm works (recommended), please click here.

Problem Statement

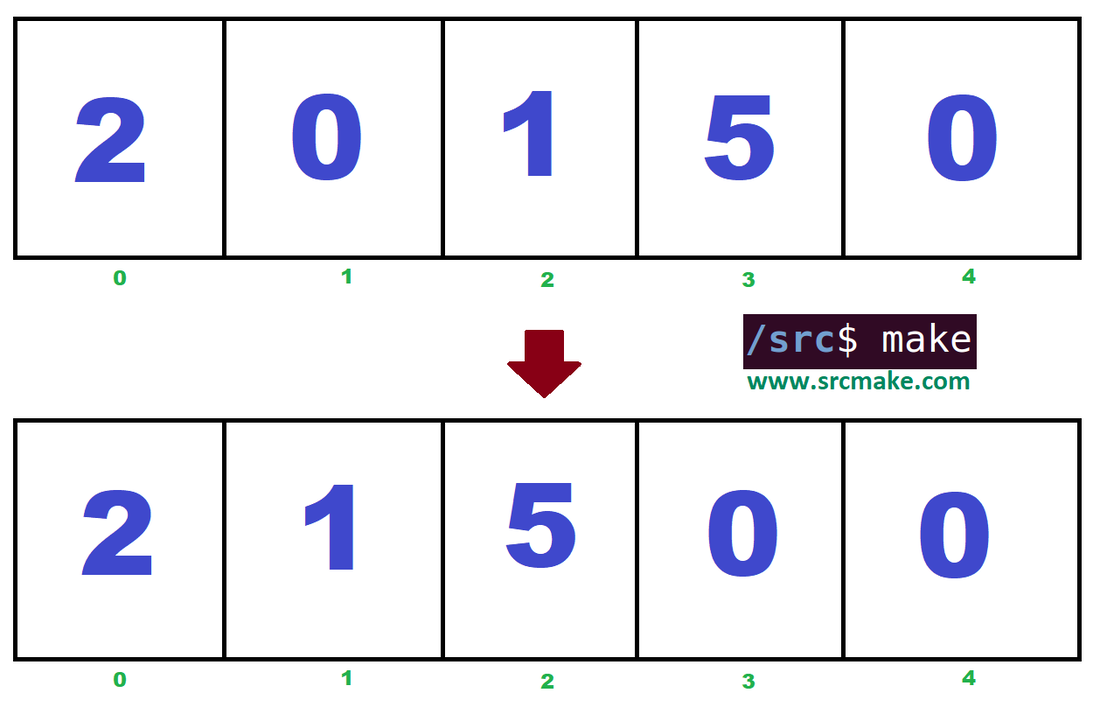
Given an array of integers, move all zeroes to the end of the array. Ideally, use no extra space, and keep the non-zero elements stable (meaning the order is preserved).

Moving the zeroes to the end of the array. Notice the other elements remain in the same order as before (stable).

---

Attempt #1: Keep Moving Zeroes To The Right - Stable | O(N^2) Time | O(1) Space

A simple algorithm is to go through the array from left to right, and every time you encounter a zero, you search the rest of the array for a non-zero to swap with. However, this approach has a bad Time complexity O(N^2) so it's not good.

Here's some pseudocode showing how you'd implement this:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

// Attempt #1: Keep moving zeroes to the right array = [2, 0, 1, 5, 0] // Go through each element in the array. for(i = 0; i < array.length; i++) { element = array[i] // We found a zero so we should shift this right. if(element == 0) { // Look for the nearest non-zero. for(j = i+1; j < array.length; j++) { nearbyElement = array[j] // This element isn't a zero, so swap it with our zero if(nearbyElement != 0) { // Swap and move on. array[i] = nearbyElement array[j] = element break } } } }

Stable: Yes
Time: O(N^2)
Space: O(1)

---

Attempt #2: Place Elements Into New Array - Stable | O(N) Time | O(N) Space

An easy approach to this question is to create a new array, and place all non-zero elements into it. Then fill the remainder of the new array with zeroes. This approach takes O(N) extra space, so it's not ideal.

Here's some pseudocode showing how you'd implement this:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

// Attempt #2: Place elements into a new array (carefully) originalArray = [2, 0, 1, 5, 0] // Initialize a new array. const newArray = [] // Go through each element in the original array. for(element in originalArray) { // If the element is a non-zero, put it in the new array. if(element != 0) { newArray.push(element) } } // Fill in the rest of the new array with zeroes. const numZeroesToFill = originalArray.length - newArray.length while(numZeroesToFill > 0) { newArray.push(0) numZeroesToFill -= 1 }

Stable: Yes
Time: O(N)
Space: ​O(N)

---

Attempt #3 (Best): Special Index Tracking - Stable | O(N) Time | O(1) Space

The ideal solution is a bit tricky. The idea is to go through the array and move all non-zero elements to the left. Where on the left do we write each non-zero element too? We'll keep track of that index basically by counting how many non-zeroes we saw so far. This is the ideal solution because the Time complexity is O(N) and the Space complexity is O(1).

Here's some C++ code for how you'd implement this:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

// This is the index we're going to be writing too. // It will be "the number of non-zero elements we've seen so far". int indexToWriteTo = 0; // Go through the array. for(int i = 0; i < array.size(); i++) { int element = array[i]; // If this element is a non-zero... if (element != 0) { // Write this element to the index we're tracking. array[indexToWriteTo] = element; // Increment our index. indexToWriteTo += 1; } } // By this line of code, the front of our array is good. // We just need to fill the end of the array with zeroes. for(int i = indexToWriteTo; i < array.size(); i++) { array[i] = 0; }

Stable: Yes
Time: O(N)
Space: ​O(1)

---

Edge Cases

1. An array with only zeroes.
2. An array with no zeroes.
3. An array starting with a zero.
4. An array ending with a zero.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

// An array with only zeroes. array = { 0, 0, 0, 0, 0 }; MoveZeroesToEnd(array); PrintArray(array); // 0 0 0 0 0 // An array with no zeroes. array = { 5, 3, 1, 2, 4 }; MoveZeroesToEnd(array); PrintArray(array); // 5 3 1 2 4 // An array starting with a zero. array = { 0, 0, 1, 7, 4 }; MoveZeroesToEnd(array); PrintArray(array); // 1 7 4 0 0 // An array ending with a zero. array = { 0, 2, 0, 0, 0 }; MoveZeroesToEnd(array); PrintArray(array); // 2 0 0 0 0

The complete code for this project can be found on my algorithm questions and answers repo on github here.

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake