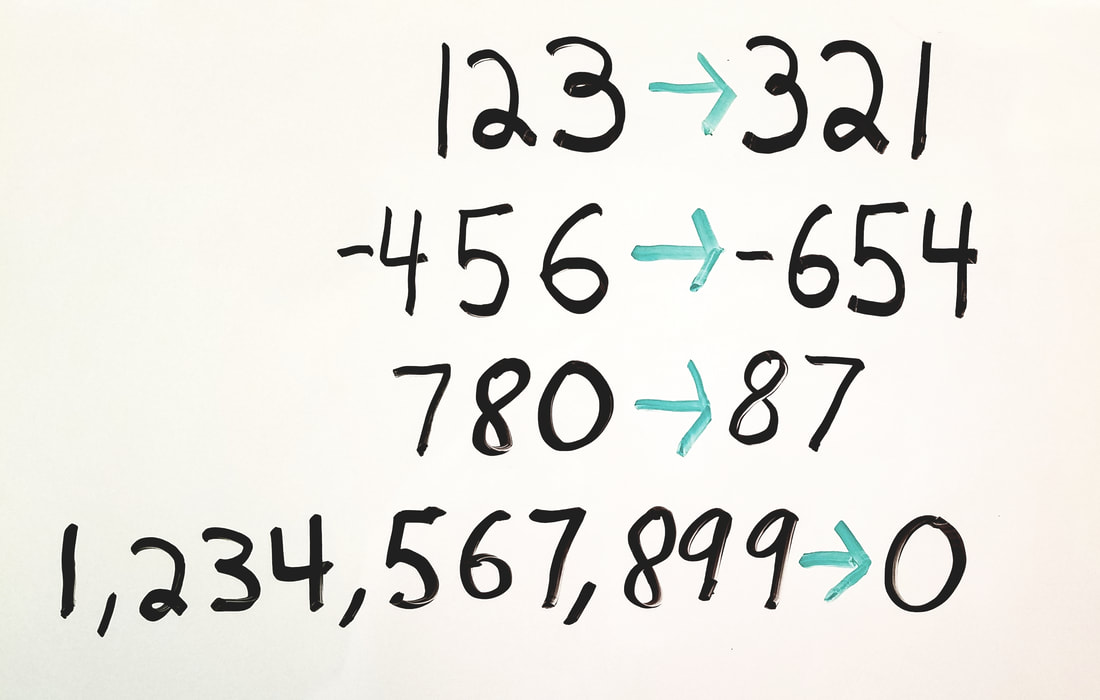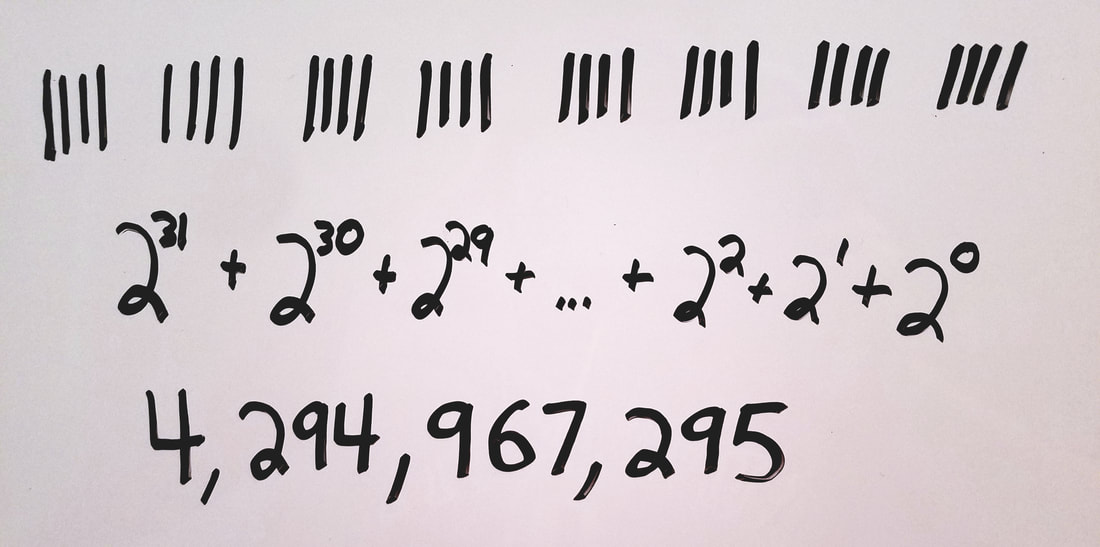To watch the youtube video that goes over this problem, click here.

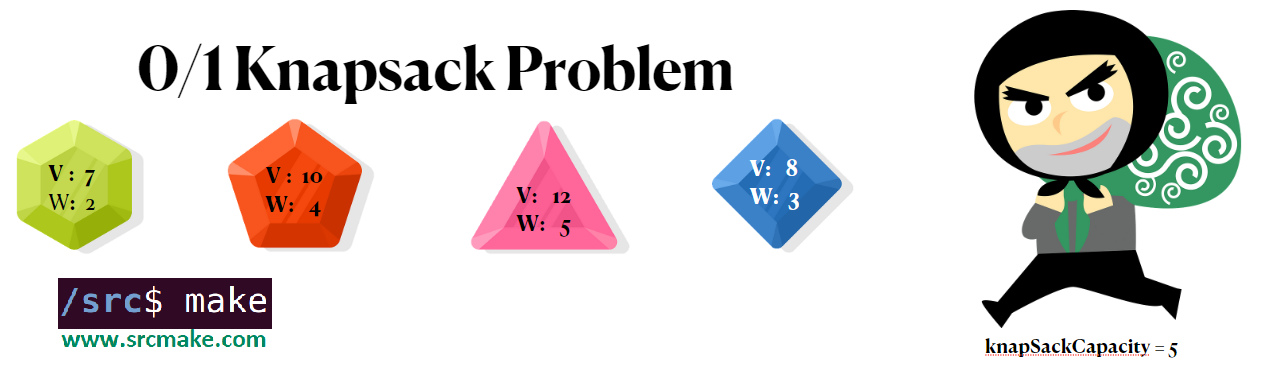
A thief is robbing a museum and he only has a single knapsack to carry all the items he steals.

​The knapsack has a capacity for the amount of weight it can hold. Each item in the museum has a weight and a value associated with it.

Given the knapsack capacity and the weight and values of the items in the museum, find the maximum value the thief can steal. (Problem on HackerRank.)

The naive solution involves keeping track of the current value and weight of the knapsack, going through each item, and trying both ways of handling the item: we either leave it behind, or pick it up (if we have enough capacity left to hold its weight).

We can code this solution with a simple recursive function. Here's the C++ code for handling the naive knapsack solution:

The time complexity is O(2^numItems) because every recursive loop has two choices.
The space complexity is O(numItems) because each recursive loop travels down to each item and so the stack space goes that high.

The dynamic programming solution, like most DP solution, involves storing the best possible answer while going through each valid solution.

In the case of the knapsack problem, the DP solution is to generate a DP table that stores the maximum value a thief can steal at each item for each valid knapsack weight.

We build this table up by going through each item/knapsackWeight combination and taking the max of the choice "take this item, or don't" and choosing the highest value.

The dynamic programming C++ code that shows how to solve the knapsack problem is as follows:

The time complexity is O(numItems*knapsackCapacity) because that's the size of the DP table.
The space complexity is O(numItems*knapsackCapacity) because that's the size of the DP table.

Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

To watch the video going over this topic, click here.

CircleCI is a service that detects when your codebase changes and runs jobs (that you define) on the code. It's used for CI/CD.

• Continuous Integration (CI) - When pushing a code change, you want to know if the state of the code is still okay. (Ex. Does the code compile (build), and do all the tests pass.) 
• Continuous Deployment (CD) - After making a code change (that hopefully passes your CI checks), deploy that code to whever it's meant to be. (Ex. Deploy a server to Heroku/AWS, or run a one-time job (ex. database migration).)

​CI/CD is incredibly useful for any project, even personal ones. The automation saves a lot of time and improves workflows, especially if you have to work with other people.

​The reasons to use CircleCI are:

• It's free
• It's not that hard to set up (compared to other CI tools)
• Many companies use CircleCI so it's good to be familiar with

In this blogpost we're going to create a simple project -> create a repo for that project on github -> setup CI with CircleCI.

Let's create a file named "main.py" and add the following code to it:

1
2
3
4
5
6
7
8

def Add(a, b):
        return a + b
        
def SayHello():
        print("sup world from srcmake")

if __name__ == '__main__':
        SayHello()

We can run this file with the following command (in your terminal):

python3 main.py

​Let's also create a file named "main-test.py" to test our main file.

1
2
3
4
5
6
7
8
9

# Import the Add function, and assert that it works correctly.
from main import Add

def TestAdd():
        assert Add(2,3) == 5
        print("Add Function works correctly")

if __name__ == '__main__':
        TestAdd()

We can run the test using the following command (in your terminal):

python3 main-test.py

Let's create a github repository for this project. Go to github and make a new repo named "circleci-demo".

Now let's push our project (which is currently on our local computer) to the github repo. (Make sure to change the username to be yours. Mine is srcmake.) In your terminal:

git init
git add .
git commit -m "Initial commit"
git remote add origin https://github.com/srcmake/circleci-demo.git
git push -u origin master

So our github repo is set up, now we want to enable CI on it by setting up CircleCI.

We need to create a configuration file so that CircleCI will know what we want it to do .

Create a folder named ".circleci" and inside of it create a file named "config.yml".

mkdir .circleci
touch .circleci/config.yml

Open ".circleci/config.yml" and add the following code:

Notice that we have two types of tasks (jobs) that we want CircleCI to do: We want to run main.py, and we want to run our tests. We're also specifying that for every branch we want to perform the build job, and the test job.

The official CircleCI Docs can show how to create more complex configurations, but this is a good starting point.

We also need to give CircleCI access to our repo so that they're authorized to run these jobs. Go to CircleCI's website, login in with your github account, and authorize them to access your circleci-demo repo that we just created. 

​Now let's push our new config file to github.

git add .
git commit -m "Adds CircleCI config file"
git push

​CircleCI should detect the code changes and run our build_and_test workflow for our branch. We should be able to see the jobs run on CircleCI's website.

(Pro-tip: If there are errors then make sure your config.yml is linted correctly. Use 2 spaces instead of tabs.)

The full source code for this project can be found here.

We have CI running now so let's test it out. Let's add a line to our unit test for our Add function to make sure 5 + 5 is equal to 10.

Check out a new branch:

git checkout -b add-test

​Add the following line of code to our TestAdd() function in "main-test.py":

assert Add(5,5) == 10

Push this branch up to github.

git add .
git commit -m "Adds test to make sure 5 + 5 is equal to 10"
git push --set-upstream origin add-test

Let's go to our github repo and make a Pull Request for this branch to see if CircleCI is running our jobs.

We should see a build job and a test job with green checkmarks since they pass. We have CI working properly.

Of course, the useful part of CI (and unit tests) is making sure our codebase is working properly. Let's see what happens if we mess up old code by making our Add function do multiplication instead of tradition. In "main.py" change our Add function to multiply instead of add.

return a * b

Commit this change and push our updated branch to github.

git add .
git commit -m "Add function now multiplies instead of adds"
git push

If we look at our Pull Request, we should see that the build step passes since the code is still functional, but now our test fails since 2 * 3 isn't 5. So now we'd know the code change being introduced by this branch is harmful and we shouldn't merge this PR (and CircleCI can use that info to stop other jobs, like making sure not to deploy if the tests fail).

CI/CD is very important, and we've seen how to use CircleCI to set up CI. Our project was very simple, but extending the project to more complicated scenarios isn't that hard once you have the base config file. And of course, setting up the CD part is as simple as adding a job to deploy and adding that to our workflow.

A few examples of how to make the most with CI/CD and CircleCI are:

• Using CircleCI to run (scheduled) cron jobs.
• Add different workflows for different branches. (Ex. We only want to deploy the master branch, but not random PR branches.)
• Set up the process to CD to a staging server.
• Ask CircleCI to run your Dockerized projects instead of needing to use native images. (For example, we used a Python base image this time.)

Keep an eye out for a more advanced CircleCI tutorial where we go through setting up the config for a Dockerized project that will also CD to a cloud host like Heroku.

Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

To watch the youtube video explaining this topic, please click here.

Given a signed 32-bit integer, reverse its digits. If there's an overflow after reversing, then return 0. (Problem on Leetcode.)

An easy solution would be to convert the integer to its string representation -> reverse that string -> convert the string back to an integer.

In the case of a negative number, we can make the number positive for the string conversion, then make it negative again before returning the final answer.

This is a pretty clean algorithm, but if you run it in Leetcode you'll likely find that your answer is wrong for some solutions. That's because this algorithm is susceptible to integer overflows.

Let's understand how an integer is represented. A 32-bit integer is literally 32 bits (0 or 1) put together in binary format.

The maximum number we can create using 32 bits is by using 32 1's, which equals 4,294,967,295.

So an unsigned 32-bit integer's maximum value is 4,294,967,295, and the range of numbers you can represent using 32 bits would be [0, 4,294,967,295].

However, a signed integer means we want to be able to include negatives numbers. The easiest way to think about this is that we want to take the maximum value for a 32-bit integer and split it in half, and allow half of the value to count toward negative numbers and the other half to count toward positive numbers.

4,294,967,295 / 2 = 2,147,483,647.5

So the range of a signed integer will be [-2,147,483,648, 2,147,483,647].

Looking back at out problem of reversing a signed 32-bit integer, if we tried to reverse 2,147,483,647 then we would get 7,463,847,412 which is definitely an overflow, since it goes over the maximum value a signed integer can be. The problem asks us to return 0 if we overflow.

One easy way to do this is to use a 64-bit (signed) integer to store the reversed value. The range for a 64-bit integer is [-9,223,372,036,854,775,808, 9,223,372,036,854,775,807], which will comfortably fit any flipped 32-bit integer.

The only difference in our code is now we work with 64-bit integers, use string_to_long, and have a couple of new if statements to check if we overflowed after reversing.

The time complexity of this solution is O(number of digits). However, this O(N) involves converting the integer to a string, reversing the string, and then converting back to a number. Those are expensive operations.

The string solution works but has expensive operations converting integers to strings and vice-versa. We can optimize by directly using math to convert the number to its reversed form.

​Basically, we go through each digit from right to left and make that the digit of our reversed number.

This solution is still O(number of digits) but the operations (modulus and divide) are less expensive.

The truth is in a real interview, if you're asked this question, the interviewer isn't going to let you use a 64-bit integer. It's basically cheating. We can't just throw more hardware (in this case, bits) at all of our problems, and we need to stay within the confines of the types we have. This is especially true for low level programming.

We can eliminate the use of 64-bit integers by, at each step, checking if we're going to overflow if we were to add the next digit.

The time complexity is still O(number of digits), but we added three if-statements at each step, so the code is going to perform slightly worse.

​​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake