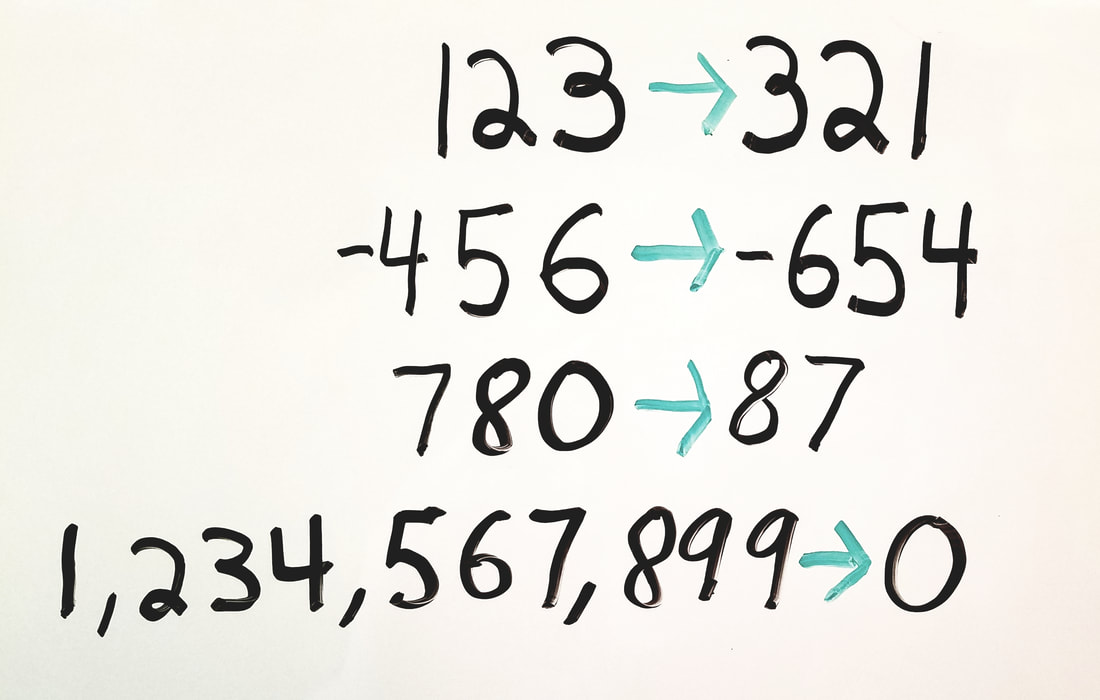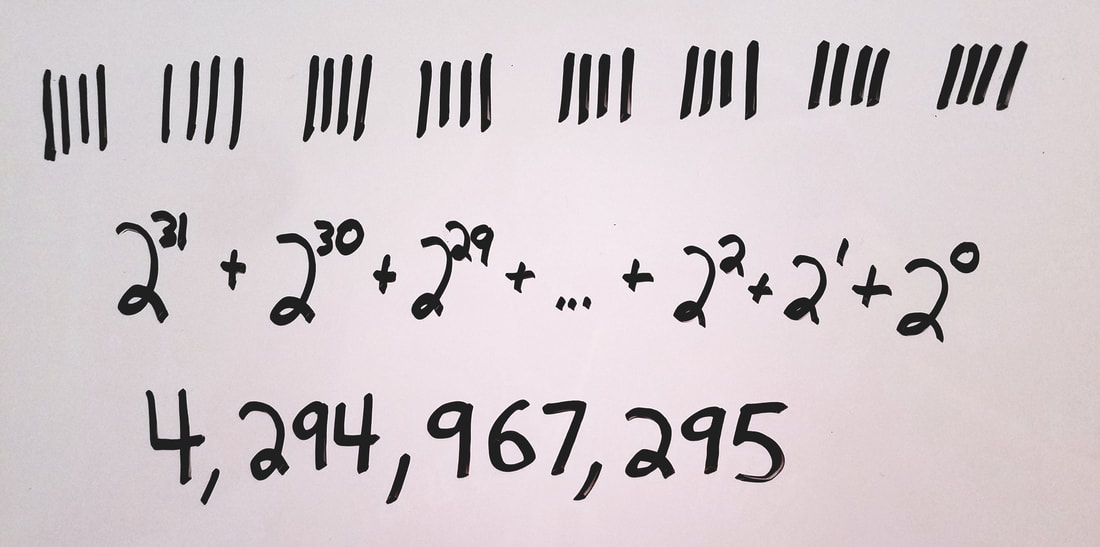[Interview Question] Reverse Integer (on Leetcode) w/ Binary Number Explanation

To watch the youtube video explaining this topic, please click here.

Problem Statement

Given a signed 32-bit integer, reverse its digits. If there's an overflow after reversing, then return 0. (Problem on Leetcode.)

---

String Solution (without Handling Overflow)

An easy solution would be to convert the integer to its string representation -> reverse that string -> convert the string back to an integer.

In the case of a negative number, we can make the number positive for the string conversion, then make it negative again before returning the final answer.

This is a pretty clean algorithm, but if you run it in Leetcode you'll likely find that your answer is wrong for some solutions. That's because this algorithm is susceptible to integer overflows.

---

An Integer's Bit Representation

Let's understand how an integer is represented. A 32-bit integer is literally 32 bits (0 or 1) put together in binary format.

The maximum number we can create using 32 bits is by using 32 1's, which equals 4,294,967,295.

So an unsigned 32-bit integer's maximum value is 4,294,967,295, and the range of numbers you can represent using 32 bits would be [0, 4,294,967,295].

However, a signed integer means we want to be able to include negatives numbers. The easiest way to think about this is that we want to take the maximum value for a 32-bit integer and split it in half, and allow half of the value to count toward negative numbers and the other half to count toward positive numbers.

4,294,967,295 / 2 = 2,147,483,647.5

So the range of a signed integer will be [-2,147,483,648, 2,147,483,647].

---

String Solution (Handling The Overflow with a 64-Bit Integer)

Looking back at out problem of reversing a signed 32-bit integer, if we tried to reverse 2,147,483,647 then we would get 7,463,847,412 which is definitely an overflow, since it goes over the maximum value a signed integer can be. The problem asks us to return 0 if we overflow.

One easy way to do this is to use a 64-bit (signed) integer to store the reversed value. The range for a 64-bit integer is [-9,223,372,036,854,775,808, 9,223,372,036,854,775,807], which will comfortably fit any flipped 32-bit integer.

The only difference in our code is now we work with 64-bit integers, use string_to_long, and have a couple of new if statements to check if we overflowed after reversing.

The time complexity of this solution is O(number of digits). However, this O(N) involves converting the integer to a string, reversing the string, and then converting back to a number. Those are expensive operations.

---

Mathematical Solution (With 64-Bit Integer)

The string solution works but has expensive operations converting integers to strings and vice-versa. We can optimize by directly using math to convert the number to its reversed form.

​Basically, we go through each digit from right to left and make that the digit of our reversed number.

This solution is still O(number of digits) but the operations (modulus and divide) are less expensive.

---

Mathematical Solution (Only Use 32-Bit Integers)

The truth is in a real interview, if you're asked this question, the interviewer isn't going to let you use a 64-bit integer. It's basically cheating. We can't just throw more hardware (in this case, bits) at all of our problems, and we need to stay within the confines of the types we have. This is especially true for low level programming.

We can eliminate the use of 64-bit integers by, at each step, checking if we're going to overflow if we were to add the next digit.

The time complexity is still O(number of digits), but we added three if-statements at each step, so the code is going to perform slightly worse.

​​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake