To watch the youtube video explaining this topic, please click here.

N-Queens is an interesting problem. It requires knowing the Backtracking algorithm to solve efficiently, and also requires a fair bit of code compared to standard algorithm questions.

In this blogpost, we'll solve the N-Queens problem. If this is your first time seeing Backtracking, please look at the previous tutorial on Backtracking on an easier problem. Additionally, our solution will show "good object oriented code" since we'll utilize a class structure to solve this (as opposed to pure code inside of functions).

Given a number n, return all valid nxn chessboards that have n queens placed on them such that no Queens are attacking each other. (Problem on Leetcode.)

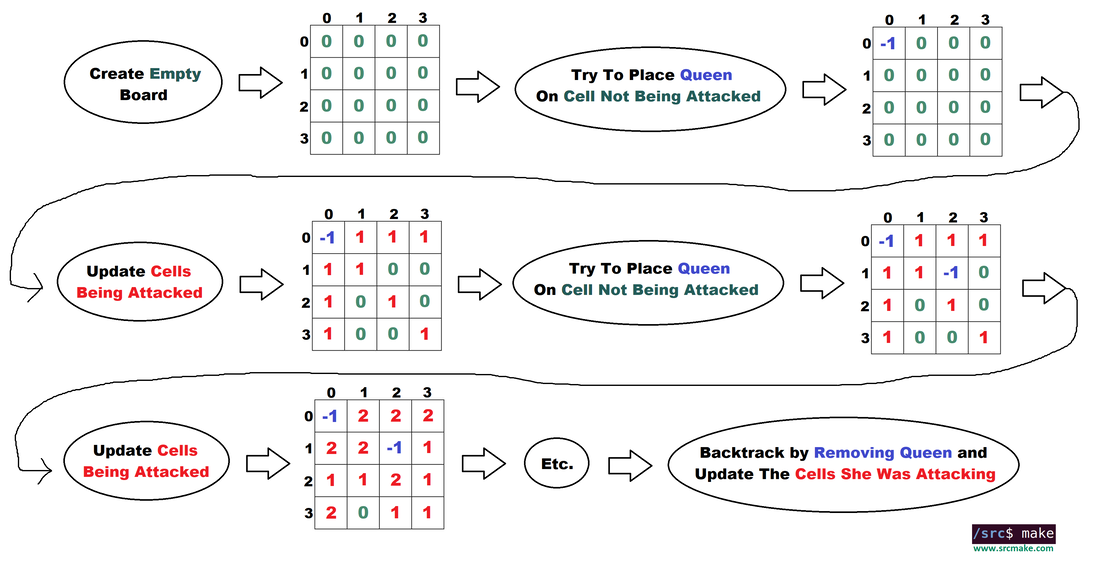
We're going to create an nxn chessboard and we continually try to place Queens on it (and if the board ends up valid with n queens on it, then we add it to our solution set), but we're going to be smart about how we place the Queens. Specifically, we're going not going to place Queens on a spots that are already being attacked. 

Let's represent the chessboard as a matrix of integers. -1 means a Queen is on a cell, otherwise the number represents the number of Queens that are attacking that cell.

The flow is to try adding Queens on a valid cell -> update the board to mark the positions she attacks, and then try adding more queens. Whenever we reach the end of a board (no more Queens can be added or we're at the final cell), we add the board if possible, and then we backtrack by removing the previous Queen we added and try placing a new Queen somewhere else.

In our case of backtracking, our shared state is the chess board, and we recursively place Queens (and update the board) and then remove that Queen (and update the board).

In addition, some optimizations we'll take advantage of are:

1. Every row needs to have exactly one Queen.
2. After placing a Queen on a tile and trying all possibilities for the rest of the board, you never need to try placing a Queen on that tile again.

​The C++ code that solves this problem is:

​​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

To watch the youtube video explaining this topic, click here.

Docker is a tool for containerizing projects so that any required dependencies (libraries) can be installed in isolation within the Docker container and doesn't have to be installed on the host computer.

This is good practice because it:

• Avoid installing unnecessary libraries/CLI tools on your computer.
• Avoids version mismatches. (Your computer has library version 2, but the project uses version 3.)
• Easier to run CI steps like building/testing.
• Easier deployments for backend servers.
• Allows for more complex projects with multiple systems. (One container could have a server, and another has a database. For complex systems, having local copies of services means easier development.)

​​In this blogpost we'll look at Dockerizing a simple project.

Your computer must have Docker installed to use it, of course. Docker installation varies depending on your operating system, so google for a guide.

This previous tutorial shows how to install Docker on older versions of Ubuntu linux.

On newer versions, of Ubuntu Linux, you can install docker using the following command:

sudo apt install docker.io

And test it with:

sudo docker run hello-world

The best projects to Dockerize are backend servers, so let's take a very basic Hello World server.

This repository has the bare minimum code required to run a Node.js server.

git clone https://github.com/srcmake/node-bare-minimum-server.git

If you have node/npm installed locally, then you can try running this project locally.

cd node-bare-minimum-server
npm install
node server.js

And go to localhost:3000 in your browser to ensure the server gives a response.

​(If you don't have node/npm installed, then don't worry because we'll be dockerizing the project in the next section to not need to have them installed locally.)

To dockerize the project, we must add a Docker file to our project.

touch Dockerfile

There are a few things we need to specify in our Dockerfile:

1. The base Docker image we're going to be copying from. (One with an OS and node/npm already installed would be nice. We can see a list here.) For production projects you can build your own base image. 
2. Specify the folder inside of the Docker image OS that our app code is going to be in.
3. Copy our project files into that folder.
4. Run anything we need to set up the project. (In our case, we need to install our npm libraries. (Note: There are some special caching tricks we could do, but this tutorial will keep it simple.)
5. Since we're running a server, we need to expose a port so connections can go into the Docker container.
6. We specify the command to run to start our server.

Open the Dockerfile and paste the following code inside of it:

Additionally, we're going to specify a Docker Ignore file, which works similarly to a Git Ignore file; it will specify files in our project folder that we don't need copied into the Docker container. (It's good practice to make the Docker container as small as possible.) For example, we don't need to copy our local node_modules folder since we want to rebuild it inside the container, anyway.

​Create the Docker Ignore file:

touch .dockerignore

Open .dockerignore and add the files/folders we don't need copied over into it:

1
2
3
4
5

/.git
/node_modules
.gitignore
LICENSE
README

Now our codebase is Dockerized. How do we run the server locally? First we need to build a Docker image for our project, and then we'll run that image.

To build the Docker image:

sudo docker build -t node-min-server .

We can see the image we just built in our list of docker images.

sudo docker images

​To run the Docker image we just built:

sudo docker run -p 8000:3000 -d node-min-server

​Note that the internal Docker container is using port 3000, but we're specifying our local computer to connect to the Docker container on our computer's port 8000. (This is just for clarity, feel free to use the same ports.)

We can now see our server running on port 8000 on our computer, without needing Node or NPM installed. Check at localhost:8000 in your browser.

And that's it. The next steps would be to commit the Dockerfile (and docker ignore file) to our project's repository and update our README for the new deployment steps.

Dockerization of a project is pretty simple and has many benefits. It's useful when working with multiple people and setting up CI/CD. All it takes to Dockerize a project is creating a Dockerfile and using a few new commands to work locally.

The next blogpost is going to be on using docker compose, which helps create more complex local systems.
We'll also be doing a tutorial on CircleCI, and Docker will help with our CI steps.

​​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

References
1. ​https://nodejs.org/fr/docs/guides/nodejs-docker-webapp/

To watch the video explaining this topic, please click here.

Backtracking is a technique when using recursion (DFS). The trick is:

1. Pass a variable around by reference (not by copy).
2. Edit the variable -> Make a recursive call -> Undo the edit.

​Basically, because DFS is deterministic and goes in a "depth-first" order, at each level we can edit information, which keeps the "state" of our system the way we need it to for the next level's recursive calls, and then we can undo the change we made for whenever we go back up to the previous level.

A good analogy of this is a kitchen. Pretend we have a kitchen that only one person is going to use at a time.

• Our mom owns the kitchen.
  • Our mom let's us use the kitchen.
  • We eat some cheese and crackers.
    • We let our friend use the kitchen.
    • Our friend uses some dishes.
    • Our friend washes those dishes.
    • Our friend stops using the kitchen and returns ownership to us.
  • We retake ownership of the kitchen.
    • We let our dad use the kitchen.
    • Our dad eats some cookies.
      • Our dad lets our uncle use the kitchen.
      • Our uncle turns the oven on.
      • Our uncle turns the oven off.
      • Our uncle stops using the kitchen and returns ownership to our dad.
    • Our dad buys some cookies to replace what he ate.
    • Our dad stops using the kitchen and returns ownership to us.
  • We buy cheese and crackers to replace what we ate.
  • We return ownership of the kitchen to our mom.
• Our mom gets the kitchen back in the exact condition she returned it to us.

As long as each person undoes the change they do when they return ownership to the person who let them use it, we can all use the same kitchen, instead of every person needing to have their own kitchen.

Similarly, using backtracking in DFS means we can have shared variable without having to create a new one for each recursive call. This saves time and memory.

Given a 2D board of tiles (letters) and a word, check if the word exists in the board.

• You may start from any tile.
• You can only travel to adjacent (up/down/left/right) tiles.
• You cannot reuse any tiles.

 (Problem on Leetcode.)

We'll try each tile as the beginning of our traversal, and what we'll recursively do is:

1. Check if the tile is valid. (In-bounds in the board ,​and matches the character in the word.)
2. Invalidate that tile by changing it to an invalid character, like "*". (Which we know will never be in our input.)
3. Recursively check the left, right, up, and down tiles.
4. Undo the tile invalidation from step 2.
5. Return the true if this tile was the end of the word or if any of the recursive calls returned true.

The "backtracking" part of this solution is that we're changing shared state (step 2), making recursive calls, and then undoing our change for when we go back up to previous levels.

Here's pseudocode for our solution to the boggle problem:

The full C++ code, which corresponds to the "Word Search" problem on Leetcode, is as follows:

​​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake