|
To watch the youtube video that goes over this topic, click here.
Introduction: Tries
A Trie is a tree data structure that stores sequences in a way such that overlapping elements (in the same position) can share the same node.
For example, "apple" and "apply" are two distinct sequences of characters, but they both share the initial sequence "appl".
A Trie is implemented as a tree. Each node of the tree holds:
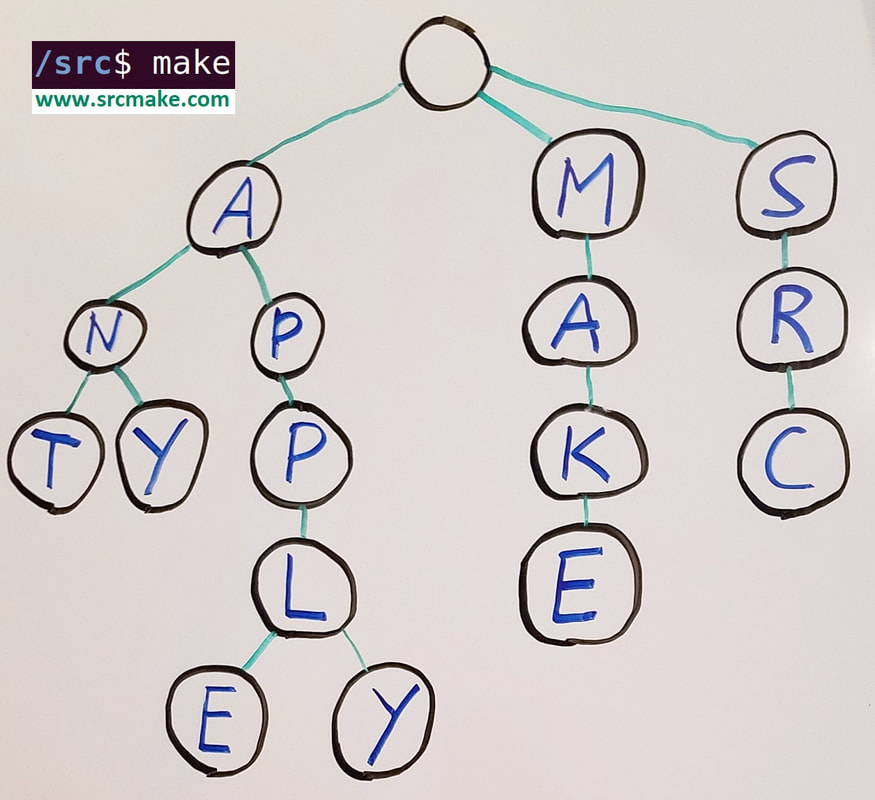
Trie's Underlying Data Model
As the picture above shows, a Trie is represented as a tree of nodes. However, unlike a binary trees where each node can just have a left and right pointer, you have to decide how many pointers each Trie node is going to have.
For example, a Trie that holds characters only containing the lowercase English alphabet will need exactly 26 pointers to other nodes. Or maybe our Trie holds phone numbers, in which case we expect only digits and each node holds 10 pointers (one for each digit). We could hardcode each pointer if we know exactly what our Trie is going to hold. We can clean this up by using an array (which still requires knowing the mapping. Ex. next[0] maps to the character 'a'). A more flexible approach (but potentially less efficient) is using a hash map, which means your Trie can scale to as many nodes as required without needing to know exactly how many ahead of time.
Now we can handle unexpected character inputs like punctuation (! ? &) or special characters.
We initialize our Trie with an empty root TrieNode, and from that rootnode we add/update nodes as necessary with methods designed to traverse and edit TrieNodes. Trie Operations (with Pseudocode)
As with most tree data structures, traversing nodes is best done with recursion or iteration. Most of the operations we'll see utilize iteration, but recursion is also fine.
Initializing the Trie
Assuming we have our TrieNode structure set up, we start by initializing an empty node to be the root of our tree. Insert If we want to insert a sequence into our Trie, we iteratively traverse the Trie for each element in the sequence. If the node doesn't exist for a certain element in the Trie, then we create it. At the last element of the sequence, we mark the node as endOfSequence=true to indicate that node ends a sequence. Contains To check if a sequence was inserted into our Trie, we iteratively traverse the Trie. If we ever find that one of the elements in the sequence doesn't have a node for it in the Trie, we return false. If we get to the end of the sequence and the node in Trie doesn't have endOfSequence==true then we return false. (This can happen in cases where we inserted longer sequences. Ex. Insert "antler" but check if our Trie contains "ant".) Prefix Exists To check if there's any sequence in our Trie that starts with a sequence, we can iteratively traverse the Trie and make sure each element of the sequence has a node in the Trie. For example, check if any sequences begin with "ant". (This is very similar to the Contains operation so code is omitted in this blog post. See the full code on github to see how it's implemented.)
The time and space complexity for all of these operations are O(number of elements in the sequence). Tries are very efficient.
To see full Trie code, see the code I wrote on github that creates a Trie class. When To Use Tries
Tries are really good data structures if you need to:
To test your knowledge, Leetcode has a problem on implementing the methods of a Trie.
Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.
Twitter: @srcmake Discord: srcmake#3644 Youtube: srcmake Twitch: www.twitch.tv/srcmake Github: srcmake
To watch the youtube video going over this topic, click here.
Introduction
Linked Lists are a fundamental data structure, and they're often asked about in interview questions. Being able to work with multiple levels of a linked list teaches you how to work with all categories of linked list problems.
In this blogpost we'll go through three layers of reversing a linked list, all of which increase in difficulty, but are related to the same base algorithm. (All of these questions are problems on Leetcode.) The problems we'll review are:
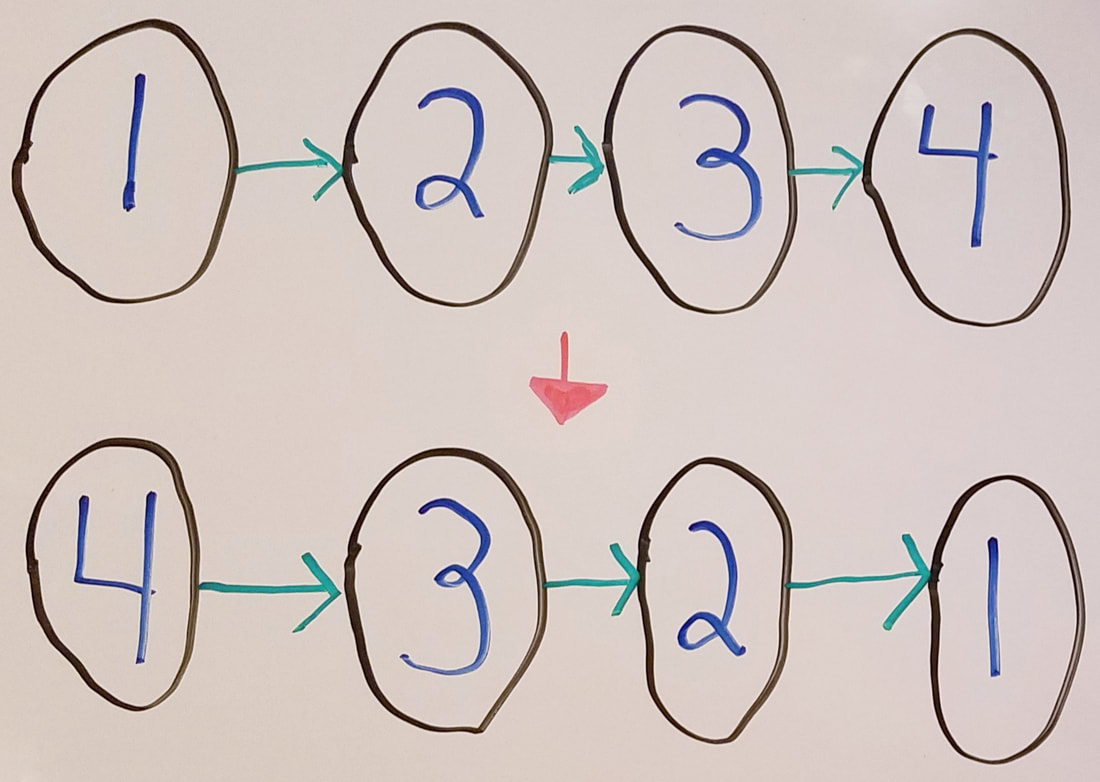
[Easy] Reverse A Linked List
Given the head of a singly linked list, reverse it. (Leetcode Problem.)
Solution (Iterative Approach)
We want to iterate through the linked list and change each node's next pointer to point to the previous node in the list.
To do this, we need too maintain two extra pointers while traversing the list, one that points to the previous node and one that points to the current node we're updating. Here's some C++ Code that does the iterative approach.
The time complexity is O(N) because we visit each node in the list once.
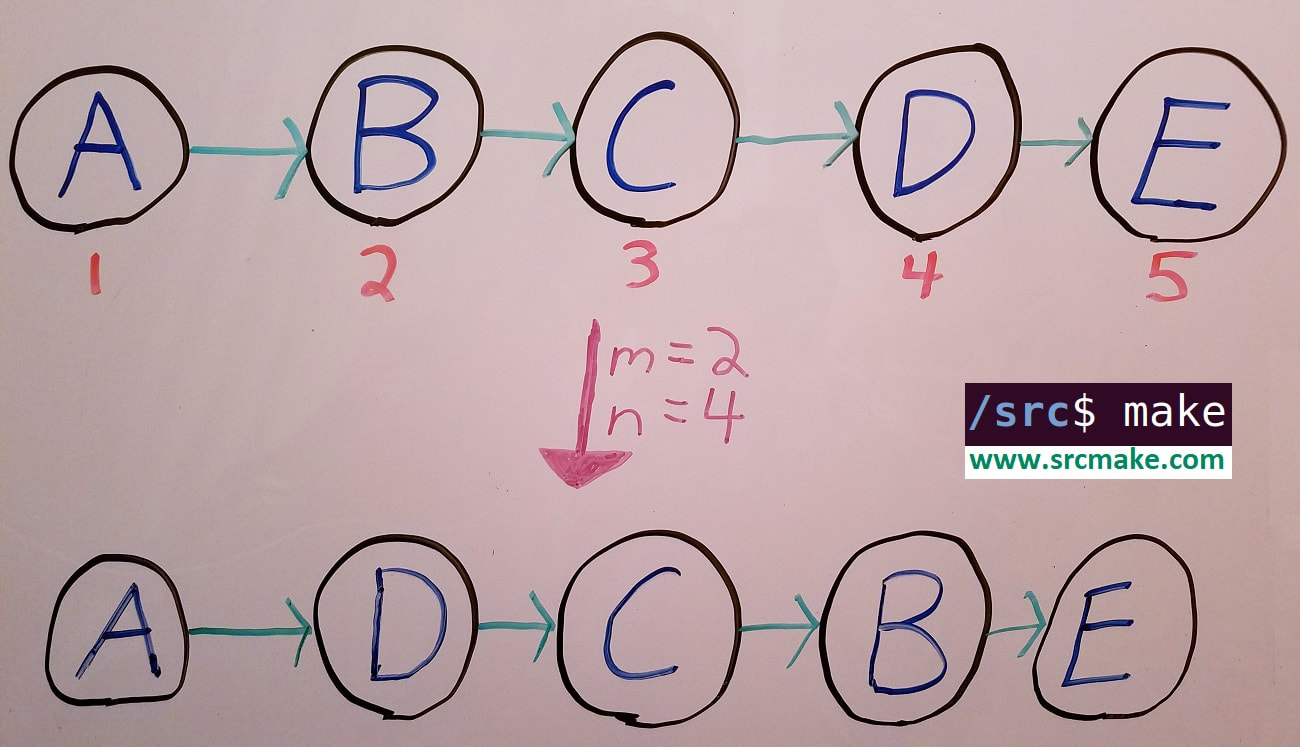
The space complexity is O(1) because the only extra data we have is three pointers. [Medium] Reverse A Linked List From Node m to Node n
Given the head of a singly linked list, reverse nodes m to n. (Problem on Leetcode.)
Solution (Iterative Approach)
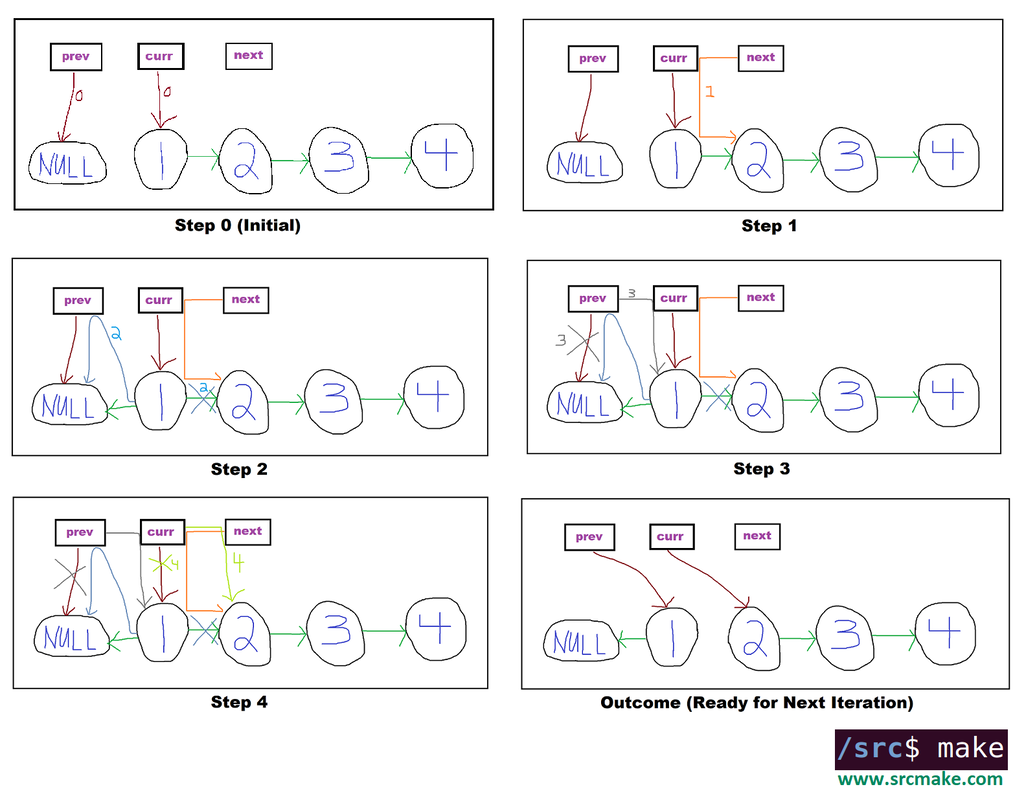
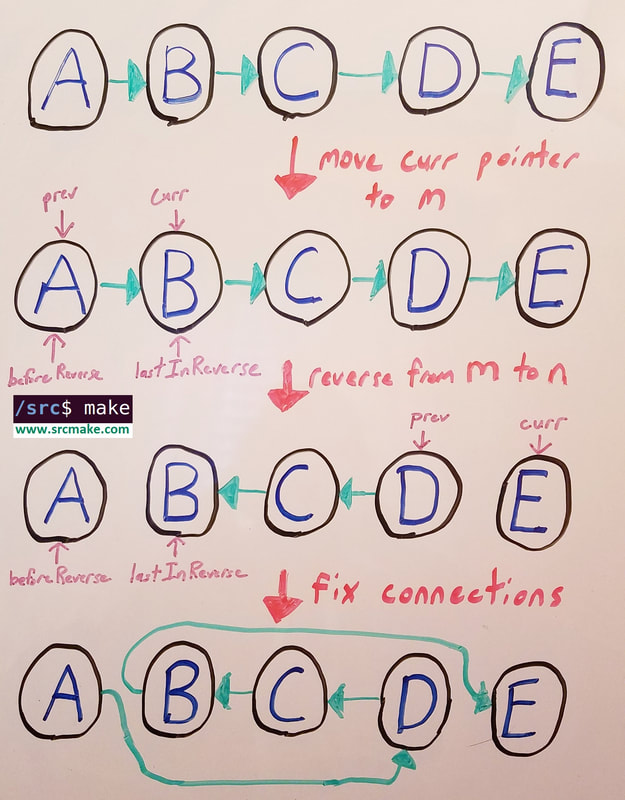
The "reversing" part is going to be the same algorithm as the base problem. The difference is, this time we have to start/stop reversing at specific nodes, and we're left with some disconnected sublists that we need to rejoin. To do this, we just need to maintain two extra pointers, one pointer to the node before the reversed chain, and one pointer to the end of the reversed chain.
The algorithm is as follows:
Here's a diagram of that algorithm in action:
Here's C++ code that implements this algorithm:
The time complexity is O(N) because we visit each node in the list once.
The space complexity is O(1) because the only extra data we have is three pointers. [Hard] Reverse A Linked List In k Groups
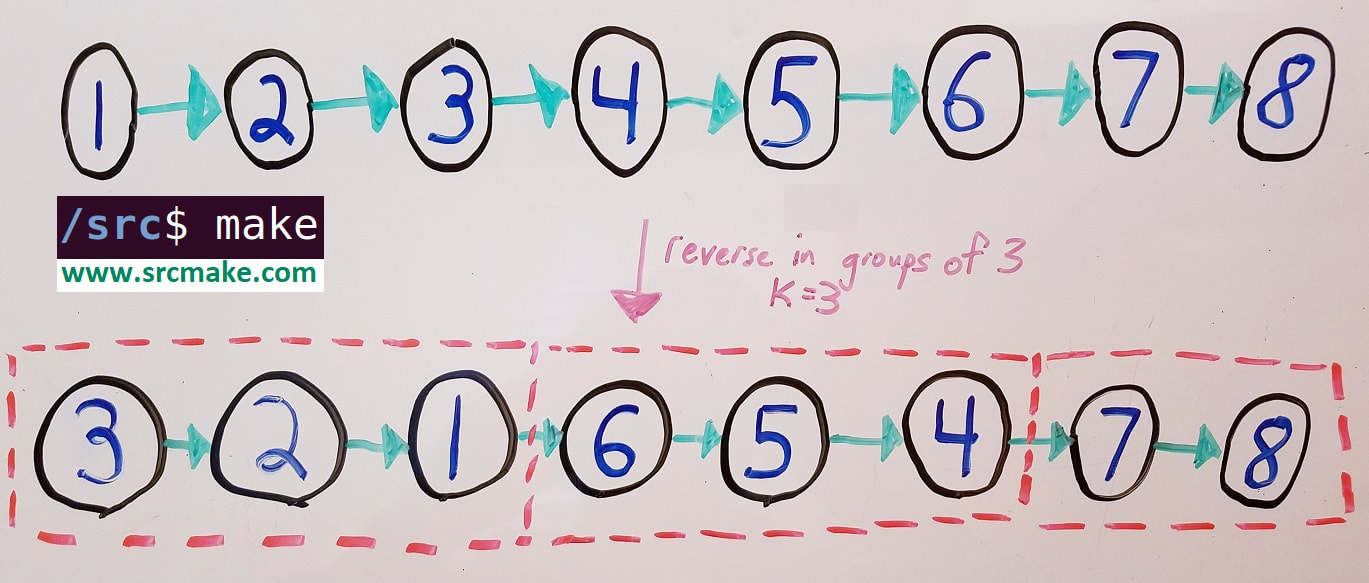
Given the head of a singly linked list, reverse groups of k-nodes at a time. If there aren't k nodes left for a group, then don't reverse them. (Problem on Leetcode.)
Solution (Iterative)
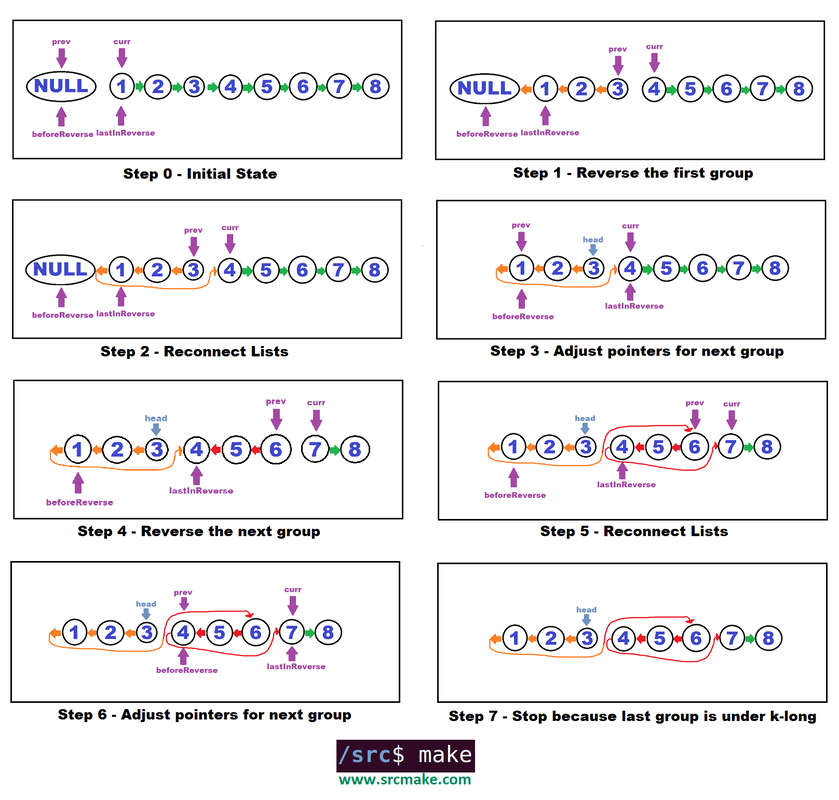
The solution to this problem builds on the previous two problems: we still use the "change next pointer to point to the previous node" reverse technique from the easy problem, and we still worry about reconnecting chains after the reversal, like the medium problem.
The difference is, this time we'll continuously reverse, starting from the head of the linked list, until we run out of k-length chains to reverse. The one thing we have to keep in mind is updating the prev pointer after each reversal chain.
Here's C++ code that implements the algorithm:
The time complexity is O(N) because we visit each node in the list twice.
The space complexity is O(1) because the only extra data we have is a few pointers and integers. Alternative Solutions
We should make note that the way we solved these problems were all through an iterative algorithm. There are three other types of algorithms possible, but they're all not ideal:
Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.
Twitter: @srcmake Discord: srcmake#3644 Youtube: srcmake Twitch: www.twitch.tv/srcmake Github: srcmake Priority Queues
Priority queues are a special data structure. They're backed by heaps (a type of binary tree), but are used like queues.
What makes a priority queue better than an ordinary queue is that the priority queue will maintain sorted order in O(logN) time even while inserting or removing new elements. The easiest way to use a priority queue is with primitive data types, such as integers and strings. However, it's possible to use priority queues on custom types, or to be able to write a custom sorting order for primitive types. Custom Comparators
Just like with sorting vectors, it's possible to use a custom comparator with priority queues, which defines how elements in the priority queue are ordered. Traditionally in C++ this is done using a struct, but lambda expressions are quicker to write and also offer the benefit of being able to reference variables outside of its scope (which is tricky to do with structs).
Here's some C++ code that uses a priority queue with a custom comparator, and the custom comparator (which is a lambda expression) is even able to make use of a hash map outside of its scope for its comparisons.
Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.
Twitter: @srcmake Discord: srcmake#3644 Youtube: srcmake Twitch: www.twitch.tv/srcmake Github: srcmake |
AuthorHi, I'm srcmake. I play video games and develop software. Pro-tip: Click the "DIRECTORY" button in the menu to find a list of blog posts.

License: All code and instructions are provided under the MIT License.
|