IBM Ponder This July 2018 Solution

To see the youtube video where I talk through the solution, click here. 

The Problem Statement

The problem statement for July 2018's IBM Ponder This challenge is as follows:

Let's call a triplet of natural numbers "obscure" if one cannot uniquely deduce them from their sum and product. For example, {2,8,9} is an obscure triplet, because {3,4,12} shares the same sum (19) and the same product (144).
​
Find a triplet of ages {a,b,c} that is obscure and stays obscure for three more years: {a+1,b+1,c+1}, {a+2,b+2,c+2} and {a+3,b+3,c+3}.

1. Note that we are asking for three *more* years, i.e. four consecutive years.

---

What We're Trying To Find

Let's restate the problem and make it as simple as possible:

• We'll think about some triplet of numbers (a,b,c).
• (a,b,c) has a sum a+b+c and a product a*b*c.
• A triplet is obscure is another triplet has the same sum and product.
• For example, the triplet (2,8,9) has sum 2+8+9=19 and product 2*8*9=144. The triplet (3,4,12) has the sum 3+4+12=19 and product 3*4*12=144. So those triplets are "obscure" because the triplet's sum and product aren't unique (another triplet can have that sum/product).
• Find some a, b, and c, where (a,b,c), (a+1,b+1,c+1), (a+2,b+2,c+2). and (a+3,b+3,c+3) are all obscure triplets.
• A bonus star is given to those who also find (a+4,b+4,c+4) and (a+5,b+5,c+5) as obscure.

Note that a, b, and c must be natural numbers (integers bigger than zero). 

---

Solving The Problem: The Logic

As far as I can tell, there's no cute mathematical trick to finding out the answer to this problem. So we'll solve this problem with programming.

Basically, our code logic is going to be this:
1. Check every possible triplet (a,b,c).
    -> Store each triplet's sum/product values.
2. Check every possible triplet (a,b,c) again.
    -> This time, check if the current triplet's sum/product values are unique, or if they match another triplet's.
    -> If they match another triplet's sum/product values, then this triplet is obscure.
        -> Since this triplet is obscure, check if (a+1,b+1,c+1) is obscure.
            -> If (a+1,b+1,c+1) is obscure, then check if (a+2,b+2,c+2) is obscure.
                -> If (a+2,b+2,c+2) is obscure, then check if (a+3,b+3,c+3) is obscure.
                    -> If (a+3,b+3,c+3) is obscure, then we found an answer.

---

The Data Structure - A 2D Table/Array

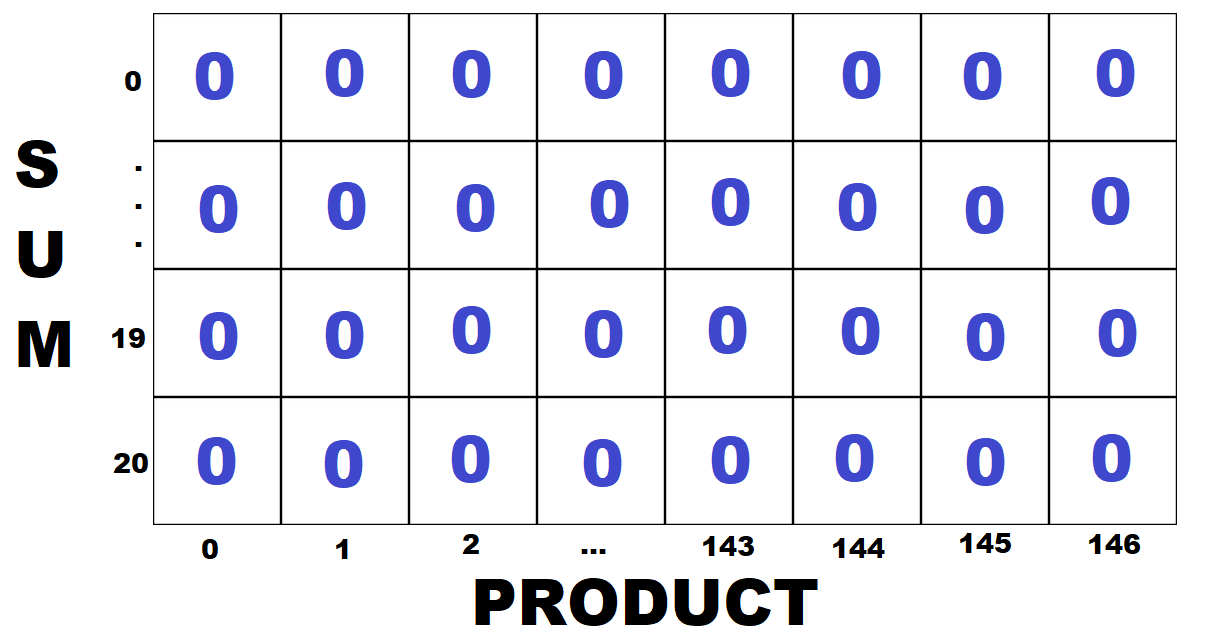
How are we going to actually store each triplet's sum/product values, and how do we check those values later? The data structure we're going to use is a simple 2D Table/Grid. (This is implemented as a 2D array/list/vector in most programming languages.)

​Each cell in our 2D table will represent the number of triplets that have a particular sum and product. Each row represents a sum value and each column represents a product value. We'll initialize our table to have all 0's. In step (1) we'll increment each cell as we find a triplet that has a sum/product, and in step (2) we'll check if a cell to see if a triplet's sum/product is unique or not.

Let's go through an example to see what this table looks like. 

Our table is initialized with all 0s.

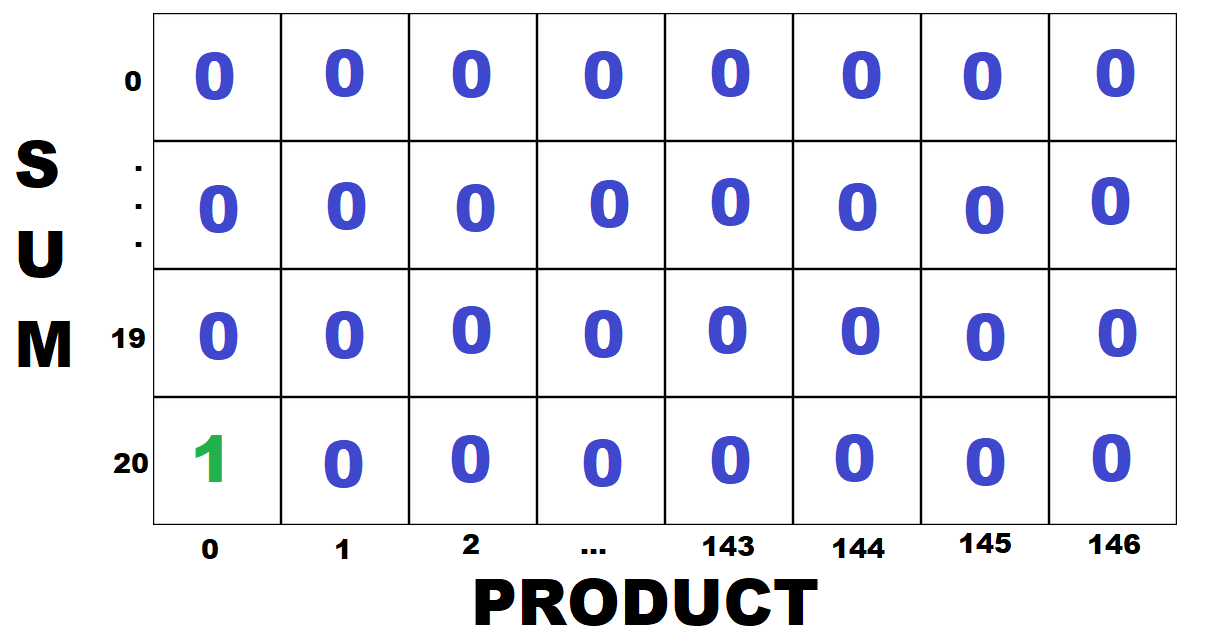
Let's say we check triplet (0, 8, 12) (even though that's not valid since 0 isn't natural). The sum is 0+8+12=20, and the product is 0*8*12=0. We increment cell [20][0] in the table by 1, representing that a triplet that we've checked has a sum of 20 and a product of 0. Our updated table looks like this:

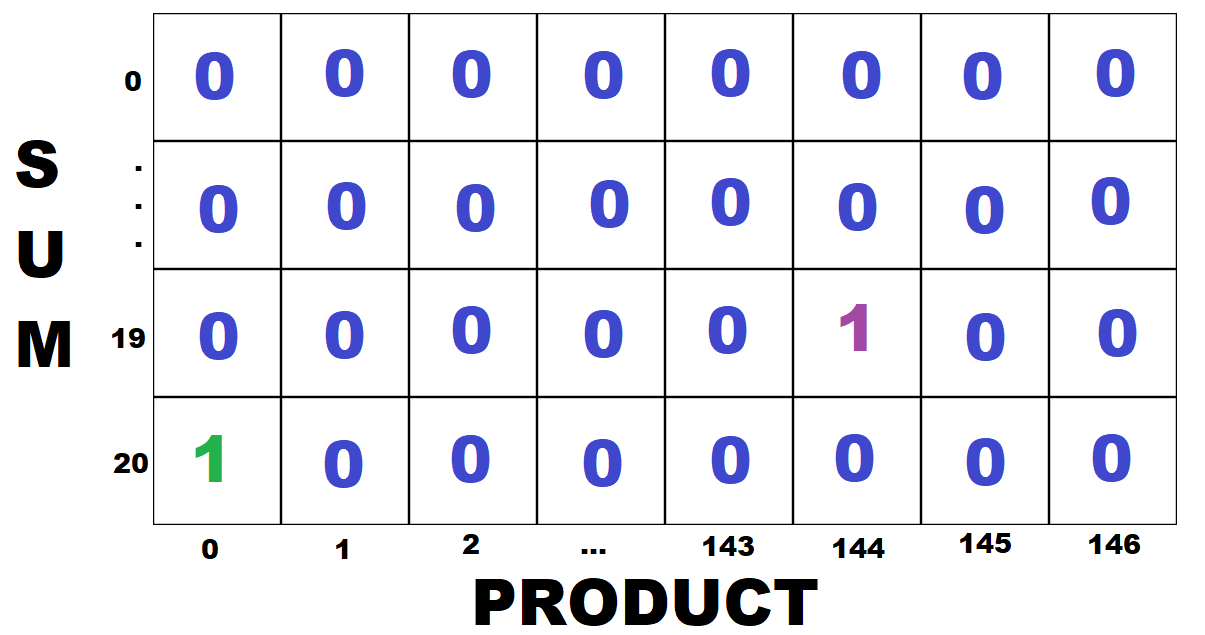
Let's say that we check triplet (2,8,9) next. The sum is 19 and the product is 144. We update cell [19][144] in our table.

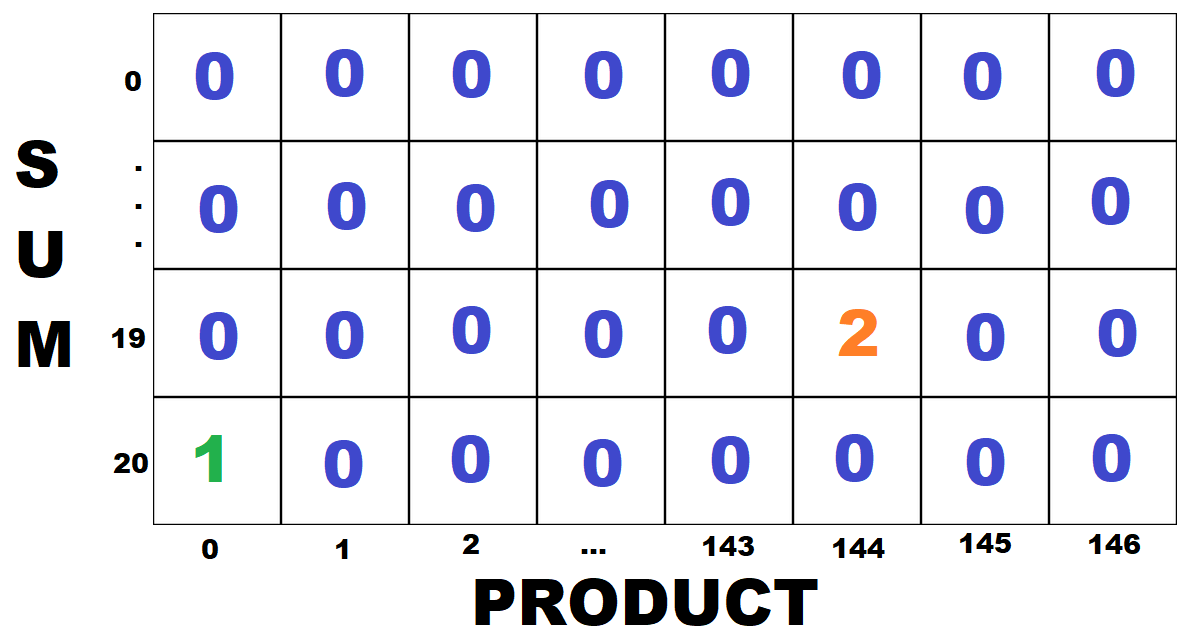
Let's say that we check triplet (3,4,12) next. The sum is 19 and the product is 144. We update cell [19][144] in our table.

And we continue with this process until we check all triplets and update all of our table. 

Then in step (2) when we check triplets again, we reference the value of a [sum][product] in the table. If the cell value is bigger than 1 (as the case with triplet (3,4,12)), then the triple is obscure.

With this data structure, storing a triplet's [sum][product] takes O(1) time and looking up whether a triplet is unique takes O(1) time. 

---

Limitations and Optimizations

Our data structure and programming logic is good enough for the normal problem, but not for a bonus star. Unfortunately, you'll find that memory limitations hold us back.

​What size is our table going to be? If we decide to check triplets starting from 1 going up to n, then our maximum sum is n+n+n and our maximum product is n*n*n. That means we need 3*n rows and n^3 columns. That's a total of 3*(n^4) space. So large n's are very tricky.

One optimization is to notice that some cells in our 2D array may be unused: we initialize a cell for every possible sum and product, even though they may go unused. A quick fix is to change our data structure: instead of using a 2D array, we can use a hash map or a red-black tree, which will only create a [sum][product] "cell" if it exists. It only changes 3 lines in our code, and helps save some space. 

---

The Code

The logic explained before is implemented in the following C++ code:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117

// Copyright srcmake.com 2018. // IBM July 2018 solution. To see blog post explanation, go to www.srcmake.com/home/ponderthisjuly2018 // http://www.research.ibm.com/haifa/ponderthis/challenges/July2018.html /* Compile and run in your terminal: g++ -std=c++11 main.cpp -o run ./run */ /* Strategy: Go through all triplets of numbers from 1 to n, and compute the sum and product for each triplet. Create a table to store whether a triplet exists for a a [sum][product] cell. Go back through all triplets and check if its particular [sum][product] cell only has a value of 1. (Meaning it's the only triplet with that sum/product value.) If yes, then check the triplets+1, +2, and +3. */ // CODE CURRENTLY USES 2D ARRAY AS DATA STRUCTURE. // To switch to red-back tree: Comment out lines 24, 33, and 44. Uncomment lines 25, 34, 45. // You can also increase the n on line 23. ///////////////////////////////////////////////////// #include <bits/stdc++.h> using namespace std; const int n = 100; // The max number we check for our triple. int table[n+n+n+1][n*n*n+1] = { 0 }; // ARRAY WAY //map<std::pair<int, int>, int> table; // RED-BLACK TREE WAY ///////////////////////////////////////////////////// ///////////////////////////////////////////////////// // Given a triple, check the table to see if it's obscure. bool IsObscure(int a, int b, int c) { if(table[a+b+c][a*b*c] > 1) { return true; } // ARRAY WAY //if(table[make_pair(a+b+c,a*b*c)] > 1) { return true; } // RED-BLACK TREE WAY return false; } ///////////////////////////////////////////////////// ///////////////////////////////////////////////////// // Tell the table that a triplet with this [sum,product] exists by incrementing it in the table. void AddToTable(int sum, int product) { table[sum][product] += 1; // ARRAY WAY //table[make_pair(sum, product)] += 1; // RED-BLACK TREE WAY } ///////////////////////////////////////////////////// ///////////////////////////////////////////////////// int main() { cout << "Program started." << endl; cout << "Going through triplets to fill tables." << endl; // For each triplet possibility.... for(int a=1; a < n; a++) { for(int b=a+1; b < n; b++) { for(int c=b+1; c < n; c++) { // Get this triplet's sum/product. int sum = a + b + c; int product = a * b * c; // Record in the table that a triplet has this sum/product value. AddToTable(sum, product); } } } cout << "Finished filling table. Now checking all triplets to find the obscure ones." << endl; // Go back through the triplets and check if they're obscure. for(int a = 1; a < n; a++) { for(int b=a+1 ; b < n; b++) { for(int c=b+1 ; c < n; c++) { if(IsObscure(a,b,c) == true) { // This triplet is obscure, so check the next three years. if(IsObscure(a+1,b+1,c+1) == true) { if(IsObscure(a+2,b+2,c+2) == true) { if(IsObscure(a+3,b+3,c+3) == true) { cout << "Four years: {" << a << "," << b << "," << c << "}" << endl; if(IsObscure(a+4,b+4,c+4) == true) { cout << "Five years: {" << a << "," << b << "," << c << "}" << endl; if(IsObscure(a+5,b+5,c+5) == true) { // The triplet's were obscure, so output this answer. cout << "Six years: {" << a << "," << b << "," << c << "}" << endl; if(IsObscure(a+6,b+6,c+6) == true) { cout << "Seven years: {" << a << "," << b << "," << c << "}" << endl; } } } } } } } } } } cout << "Program finished." << endl; return 0; } /////////////////////////////////////////////////////

Notice that the array data structure is implemented (a map in C++), but the red-black tree code is there but commented out, if you'd prefer to try that way. Read through the comments to see the exact implementation.

---

Final Answer

If you run the above code exactly as-is (which checks triplets starting from 1 up to 100), you'll get five answers. (The code runs instantly and takes up basically no space.)

​Four years: {7,30,54}                                                         
Four years: {9,21,62}                                                         
Five years: {9,21,62}                                                         
Four years: {10,22,63}                                                       
Four years: {19,21,62}                                                       
​Four years: {30,35,75}

It's that easy to get a solution this month.

You want the bonus star? Then switch the code to the red-black tree form, change n to go up to 1200, and run the code. It took my computer 10 minutes to fill the table (tree), and 17 minutes to check all of the triplets for obscurity. The program hovered around 12.5 GB of RAM (it peaked at 13.1 GB). If you do that, you'll find that (215, 328, 1053) is a triplet that stays obscure for six consecutive years. 

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake