Segment Tree Implementation - Algorithm Explained and C++ Code

To see the youtube video explaining this tutorial (which includes drawings that show how the recursion works), please click here.

Introduction - Segment Trees

Segment Trees are a tree data structure that are used to represent arrays.

Segment Trees are helpful for searching ranges in an array for certain data. For example, "find the minimum from index L to index R". 

In this article, we'll:

1. Look at the problem that segment trees are used in.
2. Look at the naive implementation for solving that problem and understand why the naive way is slow.
3. Look at how to build, query, and update a segment tree (with pseudocode).
4. Look at a C++ implementation of Segment Trees.

The segment tree representation to query for the "minimum" of the array.

---

The Problem - Repeatedly Finding The Minimum From A Range

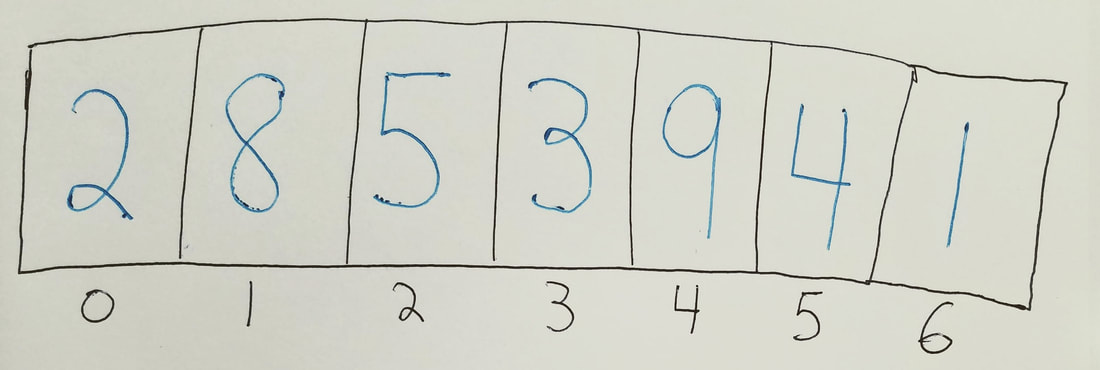
Let's say that we have the following array.

A basic array.

What's the minimum value from index 0 to index 6? -> 1
What's the minimum value from index 0 to index 5? -> 2
What's the minimum value from index 1 to index 1? -> 8
What's the minimum value from index 4 to index 5? -> 4

It's easy to find the answer to these as a human looking at this small array, but how do we write a program to solve this?

---

Naive Algorithm - Use A For Loop

The simple thing to go through each number from index L to index R and check if the number at each index is smaller than the current minimum. 

Here's some pseudocode that does that.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

// Find the minimum number for the array between indices L and R, inclusive. function RangeMinimumQuery(array, L, R) { // Initialize the min to be some huge number. minNumSoFar = someReallyBigNumber; // Search through each number between (and including) L and R for(index i = L; i <= R; i++) { currNum = array[i]; // If the current number is the smallest we've seen so far, use it. if(currNum < minNumSoFar) { minNumSoFar = currNum; } } return minNumSoFar; }

The running time of this function, used to query the array from range [L,R] is O(N), since we may be asked to query the entire array.

We don't have to do any extra work since we're given the array, so it costs O(1) extra space and O(1) time to build. And updating a value in the array costs O(1) time since we can access it's index directly.

Note: It's possible to get the query time to be smaller by memoizing results after we calculate them, but it then requires O(N^2) space/time to build the table to store the values.

These stats are pretty good, but it's possible to do even better using segment trees.

---

Segment Trees

If you're asked to make multiple queries on subranges on an array, then segment trees are the ideal data structure to use.

​The following sections will show how to build a segment tree structure, how to fill it with the appropriate values, how to query the segment tree for the value you need for a given subrange, and how to update the segment tree if a value of the original range changes.

---

Building An Empty Segment Tree

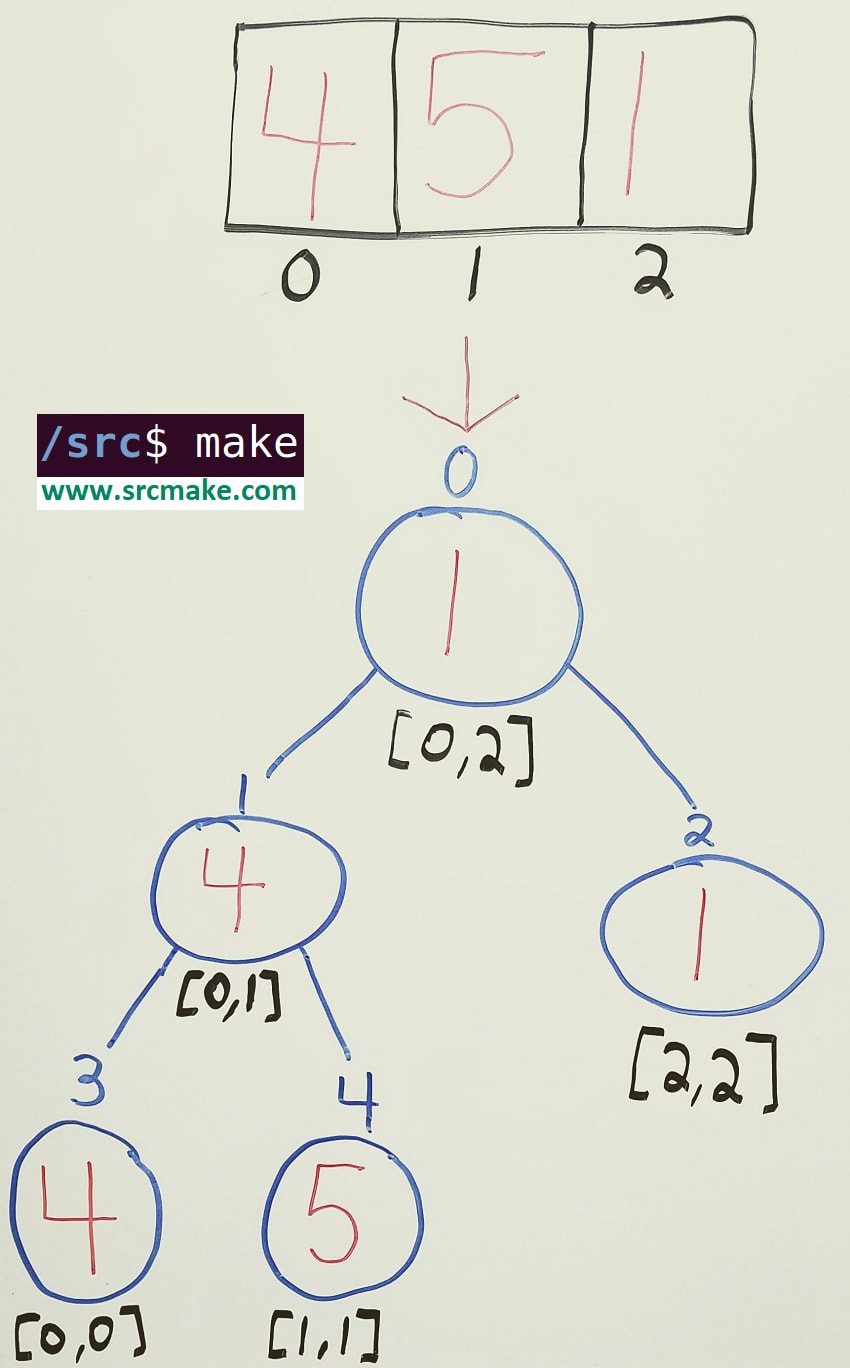
The first thing we need to do is make an empty tree. The segment tree is represented as an array, we just need to know what the size of the array is.
​
Here's the pseudocode to calculate the array size and create the array. 

1 2 3 4 5 6 7 8 9 10 11

function CreateEmptySTArray(originalArrayLength) { // Calculate the height of the tree (minus one). stHeight = ceil(log2(originalArrayLength)); // Calculate the maximum number of leaves a tree of this height can have. maxNumLeaves = (2 * (2 ^ stHeight)) - 1; // Create an array of that size. return array[maxNumLeaves]; }

This array represents our segment tree. (Each index of the array is a node in our tree.)

---

Filling In The Segment Tree With Values

 Now that we've built our segment tree, we need to fill it in with the values.

• Each node in our segment tree represents a range in the original array.
• Each node whose range represents multiple elements will have two children (ex. [0,0] only represents one element, but [0,2] represents three elements).
• A parent node will split it's range in half, and let the left child represent the first half, and the right child represent the second half. (For example a node with range [1,5] will let it's left child handle range [1,3] and let the right child handle range [4,5]. Notice if we can't evenly divide the range, we'll just put the extra element in the left child.)

With these rules in mind, we say the root node of the segment tree (at index 0 of our segment tree array) represents the range of the entire range of the original array [0, originalArrayLength]. 

To fill in the segment tree, starting at the root, we'll say that the minimum of a node is the lesser value of its two children, and so we recursively search children for their minimums. The nodes that represent just one element (ex. [4,4]), however will say it's minimum is just the single value it represents from the original array.

Here's the pseudocode implementation for filling in the segment tree.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

function RecursivelyFillMin(nodeIndex, nodeStartIndex, nodeEndIndex) { // If the range is one element long, it only has // one possible choice for the min. Fill the node. if(nodeStartIndex == nodeEndIndex) { value = originalArray[nodeStartIndex]; stArray[nodeIndex] = value; // Return this value back up to the caller. return value; } // Otherwise, find the minimum by recursively // asking this node's children. middleIndex = nodeStartIndex + ((nodeEndIndex - nodeStartIndex) / 2); leftChildNodeIndex = 2 * nodeIndex; rightChildNodeIndex = 2 * nodeIndex + 1; leftChildMin = RecursivelyFillMin(leftChildNodeIndex, nodeStartIndex, middleIndex); rightChildMin = RecursivelyFillMin(rightChildNodeIndex, middleIndex + 1, nodeEndIndex); minOfThisNode = min(leftChildMin, rightChildMin); stArray[nodeIndex] = minOfThisNode; return minOfThisNode; } function FillST() { // Starting with node 0 (the root), covering its entire range, recursively fill the stArray with its values. RecursivelyFillMin(0, 0, originalArrayLength - 1); // After the recursive call (by this line), stArray will be filled. }

The running time of filling the values in the segment tree is O(N), since we visit each element of the original array once, and we touch each leaf of the segment tree once. 

---

Querying The Segment Tree

After we've built a tree, we want to be able to search the tree for its values. (Which, in this case, is the minimum value between indices L and R.) 

Similar to the technique we used before, we recursively search the tree, starting from the root, and if a node is within the range [L, R], then we check it's value as a valid minimum of the range. 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

function RecursivelySearchForMin(L, R, nodeIndex, nodeStartIndex, nodeEndIndex) { // If this node's range is anywhere outside of [L, R] // then don't use it's value. Just return some // really big number (which wouldn't be taken as the minimum). if(nodeEndIndex < L || R < nodeStartIndex) { return reallyBigNumber; } // If this node is completely within [L, R], // then return it as the min value. if(L <= nodeStartIndex && nodeEndIndex <= R) { return stArray[nodeIndex]; } // Otherwise this node is partially within [L, R]. // (Recursively) check this node's children and return the min of those two. middleIndex = nodeStartIndex + ((nodeEndIndex - nodeStartIndex) / 2); leftChildNodeIndex = 2 * nodeIndex; rightChildNodeIndex = 2 * nodeIndex + 1; leftChildMin = RecursivelySearchForMin(L, R, leftChildNodeIndex, nodeStartIndex, middleIndex); rightChildMin = RecursivelySearchForMin(L, R, rightChildNodeIndex, middleIndex + 1, nodeEndIndex); minOfThisNode = min(leftChildMin, rightChildMin); return minOfThisNode; } // Find the minimum value between indices L and R. function FindMin(L, R) { // Recursively search the tree, starting from the root (node 0). min = RecursivelySearchForMin(L, R, 0, 0, origArrayLength - 1); return min; }

The running time of this operation is O(log N). At worst, we'll have to go down the height of the tree twice, once for the left subtree, and one for the right subtree.

---

Updating A Value In The Segment Tree

If one of the elements of the original array needs to be updated with a new value, then we simply go through that element's direct path in the segment tree and update the minimum accordingly.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

function RecursivelyUpdateST(newValue, newValueIndex, nodeIndex, nodeStartIndex, nodeEndIndex) { // If the start index equals the end index, then this node represents the exact value from the original array. // We must update this value with the new value (since the old one got replaced). if(nodeStartIndex == nodeEndIndex) { stArray[nodeIndex] = newValue; return; } // Otherwise, if check either the left or right subtree to find the index that got updated. middleIndex = nodeStartIndex + ((nodeEndIndex - nodeStartIndex) / 2); leftChildNodeIndex = 2 * nodeIndex; rightChildNodeIndex = 2 * nodeIndex + 1; // If the updated index is in the left subtree... if(nodeStartIndex <= newValueIndex && newValueIndex <= middleIndex) { // Recursively update left subtree. RecursivelyUpdateST(newValue, newValueIndex, leftChildNodeIndex, nodeStartIndex, middleIndex); } // If it's not in the left, then update the right subtree, instead. else { // Recursively update right subtree. RecursivelyUpdateST(newValue, newValueIndex, rightChildNodeIndex, middleIndex + 1, nodeEndIndex); } // We can look for the children's min's directly from the ST. minFromLeftChild = stArray[leftChildNodeIndex]; minFromRightChild = stArray[rightChildNodeIndex]; // The min of this node is the min between its two children. // (One of which might have been updated.) minOfThisNode = min(minFromLeftChild, minFromRightChild); stArray[nodeIndex] = minOfThisNode; } function UpdateValue(newValue, newValueIndex) { // Recursively go through the tree starting at the root (node 0), // and check if any nodes (within this newValue index's range) // need to be updated because the newValue is the new minimum for it. RecursivelyUpdateST(newValue, newValueIndex, 0, 0, origArrayLength - 1); }

The running time is O(log N), since we only need to travel the height of the segment tree once. (The leaf node representing the updated index, up to the root of the tree.)

---

Adding/Deleting A Value In The Array

Basically, if you have to add a new value to the original array, then you have to construct a brand new segment tree. This ends up costing O(N) time to build the new tree. (Don't forget to delete the old tree.)

---

---

C++ Segment Tree Full Class Implementation

A full Segment Tree C++ implementation can be found on github here: https://github.com/srcmake/segment-tree

​Note that the code was meant to be readable for this tutorial, and not necessarily "efficient". (Meaning some operations could be improved, or some code could be moved to functions. (Ex. Calculating the middle index.))

​Here's a sample of the class definition (inside a file named segment-tree.hpp):

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

namespace srcmake { //////////////////////////////////////////////////////////// /////////// SegmentTree Class Definition /////////////////// template<class T> class SegmentTree { private: T* st; // A pointer to the root of the ST. int stArrayLength; // The length of the st array. (Num leaves.) int originalArrayLength; // The length of the original array. void AllocateEmptyST(const std::vector<T>&); // Allocate the space for an empty ST. void DeallocateST(); // Delete the ST previously created. void FillInST(const std::vector<T>&);// Fill the ST with the proper values. T RecursivelyFillST(int, int, int, const std::vector<T>&); // Recursively find, set, return min of node. T RecursivelySearchForMin(int, int, int, int, int); // Recursively search a node from L to R for it's children's min values (if necessary). void RecursivelyUpdate(int, T, int, int, int); // Recursively update a node with the newValue if it's within the node's range. public: SegmentTree(std::vector<T>); // Constructor ~SegmentTree(); // Destructor T query(int, int); // Query a range from L to R. void update(int, T); // Update an index to the new value T. void print(); // Print the current segment tree (in-order). }; // class SegmentTree //////////////////////////////////////////////////////////// //////////////////////////////////////////////////////////// } // namespace srcmake

The code is similar to our pseudocode, with a few private variables included. (The definitions for each function can be found in the actual segment tree class file on github.
An example of using this class is...

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

// Copyright srcmake 2019. #include <iostream> #include <vector> #include "segment-tree.hpp" using namespace std; int main() { cout << "Program started.\n"; //////////////////////////////////////////////////////////// // Our initial range. vector<int> v2 = { 2, 8, 5, 3, 9, 4, 1 }; // Instantiate our segment tree data structure. srcmake::SegmentTree<int> srcmakeSegmentTree2 = srcmake::SegmentTree<int>(v2); // Print the tree (in-order heap version) so we can see it. srcmakeSegmentTree2.print(); // An example query. int L = 0; int R = 6; cout << "Min from " << L << " to " << R << " is " << srcmakeSegmentTree2.query(L, R) << ".\n"; //////////////////////////////////////////////////////////// cout << "Program finished.\n"; }

---

Extending Segment Tree for Other Problems

This tutorial showed a Segment Tree designed for Range Minimum Queries (RMQ), specifically for storing integers, but of course segment trees can be extended for more than just finding the minimum.

We can also:

• Find the maximum in a range. (Range Maximum Query)
• Find the sum of a range.
• Return the index of a a minimum/maximum value, instead of the value itself.
• We can store objects in the segment tree, not just numbers.

---

Conclusion

Segment trees are a data structure that comes up in algorithm competitions (and there's usually no time to code one from scratch), so it's better to have the code ready beforehand to copy and paste. So bookmark this blogpost, subscribe on youtube, and star the github repo.

Keep in mind that this tutorial was meant for demonstration purposes, and there are optimizations and edge cases we could've covered. Feel free to experiment with those on your own.

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

References
1. https://www.geeksforgeeks.org/segment-tree-set-2-range-maximum-query-node-update/
​2. https://www.hackerearth.com/practice/data-structures/advanced-data-structures/segment-trees/tutorial/
3. www.geeksforgeeks.org/segment-tree-efficient-implementation/