Interview Question: Which Sorting Algorithm Is Best? (With C++ Code)

To see the 10 minute youtube video that talks through this topic, click here.

What's The Best Sorting Algorithm

Sometimes we need to sort our data. Maybe we have a list of names, or a list of numbers, and we want them to be in order.

There are many different sorting techniques/algorithms, but some are better than others. (And in an interview, you may be asked which is best.) There is no best sorting algorithm, it depends on the data/situation. But let's look at when to use each sorting algorithm.

Factors In Deciding A Good Sorting Algorithm

Running Time - How quick is an algorithm? We care about average and worst case scenarios. O(N) is godly, O(NlogN) is the standard, O(N^2) is bad, usually.
Space - How much extra space does a sorting algorithm need? (In-place means no extra space is required, which is good.)
Stable - Will the order of same-data-points be preserved? For example, in [2, 4(a), 1, 5, 4(b), 3] if the first 4 (labeled as 4(a)) ends up before the second 4 (labeled as (4b)) in the sorted array, like [1, 2, 3, 4(a), 4(b), 5], then the sorting algorithm is stable.
Swaps - There's a cost associated with swapping two elements in an array/list. If swapping is expensive, then we may want to choose an algorithm that does as few swaps as possible.
Is the data already sorted? - Sometimes, the data isn't randomly organized, which affects how an algorithm performs. For example, maybe we have a sorted list, and add a few numbers at the end of it. Some algorithms do better on mostly-sorted data than others.
Will the data fit in RAM? - Sometimes we have to sort data that's so huge that it won't fit into RAM, meaning we need to use a special algorithm that will work on data stored on a hard drive.

Top-Tier Sorting Algorithms

There are a lot of sorting algorithms out there, but since we're only looking at this for the sake of an interview question, we'll go over four good ones.

Selection Sort - The simplest sorting algorithm: Start at the first element of an array. Search through all the elements left in the array, and keep track of which one is the smallest. If the smallest number found is smaller than the current element, swap them. Then move to the next element in the array. Time: O(N^2). Space: O(1). Stable: No. Swaps: O(N). If data is already sorted: O(N^2). Selection sort is simple, but only useful if swaps are expensive.
Insertion Sort - Go through each element in the array. If the current element is smaller than the element to it's left, swap it left (until it's bigger than the element to it's left). Time: O(N^2). Space: O(1). Stable: Yes. Swaps: O(N^2). If the data is already sorted: O(N). Insertion sort is excellent if there's an already sorted list, and a bit of data is added to the end of it (and then you need to resort the whole list).
Merge Sort - Merge sort cuts an array in half, forming two subarrays. It cuts those subarrays in half, and repeats the process until the subarrays are one element in size. Merge sort then merges the subarrays by selectively choosing the smallest elements to put in first, and builds the subarrays back up in size until the full array is recreated, in sorted form. Time: O(NlogN). Space: O(N). Stable: Yes. If the data is already sorted: O(NlogN). Merge sort is great, and the technique is good for data on hard drives that can't fit in RAM.
Quick Sort - Choose an element as the "pivot" element, and go through the array, moving all elements smaller than the pivot to the left, and all the larger elements to the right. Then put the pivot in between those elements. Then, for each "left" and "right" subarray, do the same process of picking a pivot and moving elements around. Time: O(N^2) in the worst case, but usually acts like O(NlogN). Space: O(1). Stable: No. If the data is already sorted: O(N^2) depending on what your pivot element is. Quick sort is usually faster than merge sort, so typically it's used. But it does have a worst case of O(N^2) so don't choose it if we absolutely need O(NlogN) to be guaranteed. (P.S. In the real world, most quick sort algorithms randomize the dataset before sorting it, to help avoid the worst case.)

Here's the code for those sorting algorithms.

// Copyright srcmake.com 2018.
// C++ Sorting Algorithm Examples
// C++ Selection Sort, C++ Insertion Sort, C++ Merge Sort, C++ Quick Sort
// Official webpage for this tutorial: https://www.srcmake.com/home/sorting

/* Compile with:
g++ -std=c++14 main.cpp -o run
./run
*/

/* Note: We're passing our input vector to the 
algorithm function in a way that it'll be copied. 
In real life, you'd pass the vector by reference. */

#include <iostream>
#include <vector>
using namespace std;

//////////////////////////////////////////////////////
////// PRINT A VECTOR //////
// Print a vector to stdout.
void PrintVector(vector<int> &a, string sortname)
    {
    cout << "Printing " << sortname << ": ";
    // Add a tab to make it look more presentable.
    if(sortname != "Selection sort" && sortname != "Insertion sort") { cout << "\t "; }
    for(int i = 0; i < a.size(); i++)
        {
        cout << a[i] << " ";
        }
    cout << endl;
    }
/////////////////////////////////////////////////////

    
//////////////////////////////////////////////////////
////// SELECTION SORT //////
// Running time: O(N^2). Space Required: O(1) Stable: No.
void SelectionSort(vector<int> a)
    {
    // Go through each element of the vector.
    for(int i = 0; i < a.size(); i++)
        {
        int currNum = a[i];
        int currIndex = i;
        
        // Search for the minimum element in the rest of the array.
        int minNum = a[i]; // Default it to the current element being min.
        int minIndex = i; 
        
        for(int j = i+1; j < a.size(); j++) // Every element after the current.
            {
            int num = a[j];
            int index = j;
            
            // If this element is smaller than the minimum so far, update the min variable.
            if(num < minNum)
                {
                minNum = num;
                minIndex = index;
                }
            }
        
        // We found the minimum number. Perform the swap.
        // (It's fine if the current element is the minimum.)
        int temp = currNum;
        a[currIndex] = minNum;
        a[minIndex] = temp;
        }
        
    // Output the sorted vector.
    PrintVector(a, "Selection sort");
    }
/////////////////////////////////////////////////////


//////////////////////////////////////////////////////
////// INSERTION SORT //////
// Running time: O(N^2). Space Required: O(1). Stable: Yes.
void InsertionSort(vector<int> a)
    {
    // Go through each element of the array (we don't need to check the first).
    for(int i = 1; i < a.size(); i++)
        {
        int currNum = a[i];
        int currIndex = i;
        
        // If the current element is smaller than the element to it's left (and a left element exists)...
        while(currNum < a[currIndex-1] && currIndex > 0)
            {
            int leftIndex = currIndex-1;
            int leftNum = a[leftIndex];
            
            // Swap the current number and it's left number.
            a[leftIndex] = currNum;
            a[currIndex] = leftNum;
            
            // Update the currIndex for the next iteration of this while loop.
            currIndex = leftIndex;
            }
        }
        
    // Output the sorted vector.
    PrintVector(a, "Insertion sort");
    }
/////////////////////////////////////////////////////


//////////////////////////////////////////////////////
////// MERGE SORT //////
// Running time: O(NlogN). Space Required: O(N) Stable: Yes.
// Help from: https://www.geeksforgeeks.org/merge-sort/
void Merge(vector<int> &a, int startIndex, int middleIndex, int endIndex)
    {
    // Size of the two subarrays.
    int n1 = middleIndex - startIndex + 1;
    int n2 = endIndex - middleIndex; 
    
    // Create temporary vectors.
    vector<int> L(n1);
    vector<int> R(n2);
    
    // Copy the data in a to our temp vectors.
    for(int i = 0; i < n1; i++)
        { 
        L[i] = a[startIndex + i]; 
        }
    for(int i = 0; i < n2; i++)
        { 
        R[i] = a[middleIndex + 1 + i]; 
        }
    
    // Merge the temp vectors back into a.
    int leftIndex = 0;            // Initial index of the first subarray.
    int rightIndex = 0;            // Initial index of the second subarray.
    int mergedIndex = startIndex; // Initial index of the merged array.
    
    // Selectively choose the smallest element from the subarrays to put into the merged array. 
    while(leftIndex < n1 && rightIndex < n2)
        {
        int leftNum = L[leftIndex];
        int rightNum = R[rightIndex];
        
        // The left number is smaller, so put it in the merged array.
        // And increment the index.
        if(leftNum <= rightNum)
            {
            a[mergedIndex] = leftNum;
            leftIndex++;
            }
        // The right number is smaller, so put it in the merged array.
        else
            {
            a[mergedIndex] = rightNum;
            rightIndex++;
            }
        mergedIndex++;
        }
    
    // Copy any remaining elements in the left and right subarrays, if there are any.
    while(leftIndex < n1)
        {
        a[mergedIndex] = L[leftIndex];
        leftIndex++;
        mergedIndex++;
        }
    while(rightIndex < n2)
        {
        a[mergedIndex] = R[rightIndex];
        rightIndex++;
        mergedIndex++;
        }
    }

void Divide(vector<int> &a, int startIndex, int endIndex)
    {
    // This (sub)array is bigger than 2 elements, so divide it.
    if(startIndex < endIndex) 
        {
        int middleIndex = (startIndex + endIndex)/2;
        
        // Recursively divide the two subarrays we can form from this.
        Divide(a, startIndex, middleIndex);
        Divide(a, middleIndex+1, endIndex);
        
        // Now merge these two subarrays together.
        Merge(a, startIndex, middleIndex, endIndex);
        }
    }

void MergeSort(vector<int> a)
    {
    // Divide needs to be called recursively.
    // We begin by dividing a from the first index to the last.
    Divide(a, 0, a.size()-1);    
        
    // Output the sorted vector.
    PrintVector(a, "Merge sort");
    }
/////////////////////////////////////////////////////


//////////////////////////////////////////////////////
////// QUICK SORT //////
// Running time: O(NlogN). Space Required: O(N) Stable: Yes.
int Partition(vector<int> &a, int startIndex, int endIndex)
    {
    // Choose our pivot as the last element in the array.
    int pivotNum = a[endIndex];
    int pivotIndex = endIndex;
    
    // The index of our "wall".
    // Left of the wall means smaller elements than the pivot.
    // Right of the wall means bigger elements than the pivot.
    int wallIndex = startIndex-1;
    
    // Go through each element in this subarray.
    for(int i = startIndex; i <= endIndex-1; i++)
        {
        int currNum = a[i];
        int currIndex = i;
        
        // If the current element is smaller than (or equal to) the pivot...
        if(currNum <= pivotNum)
            {
            // Increment our wallIndex. (Move our wall to the right.)
            wallIndex++;
            // The number at the wall.
            int wallNum = a[wallIndex];
            // Swap the current element and whatever is right of the wall (which is at the new wallIndex).
            a[wallIndex] = currNum;
            a[currIndex] = wallNum;
            }
        }
    
    // Finally, move our pivot number to the right of the wall (in between the subarrays).
    wallIndex++;
    int wallNum = a[wallIndex];
    a[wallIndex] = pivotNum;
    a[pivotIndex] = wallNum;
    
    // Return the index of the pivot (which is now the wallIndex.
    return wallIndex;
    }

void QDivide(vector<int> &a, int startIndex, int endIndex)
    {
    // If the subarray is bigger than one element in size...
    if(startIndex < endIndex)
        {
        // Partition the array.
        int pivotIndex = Partition(a, startIndex, endIndex);
        
        // Recursively divide and partition the two subarrays.
        QDivide(a, startIndex, pivotIndex-1);
        QDivide(a, pivotIndex+1, endIndex);
        }
    }

void QuickSort(vector<int> a)
    {
    // Recursively divide the vector. Start from the beginning and the end.
    QDivide(a, 0, a.size()-1);
    
    // Output the sorted vector.
    PrintVector(a, "Quick sort");
    }
/////////////////////////////////////////////////////

    
//////////////////////////////////////////////////////
////// MAIN //////
int main() 
    {
    cout << "Program started.\n";
    
    // Let's create an unsorted array (vector).
    vector<int> a = {3, 5, 1, 3, 4, 8, 1, 7, 11, 9, 2, 5, 6, 1};
    
    // Print our unsorted vector out.
    PrintVector(a, "Unsorted");
    
    // Call each of our sorting algorithms (function) on our vector.
    SelectionSort(a);
    InsertionSort(a);
    MergeSort(a);
    QuickSort(a);
    
    cout << "Program ended.\n";
    return 0;
    }
//////////////////////////////////////////////////////

You can download the code from github, here.

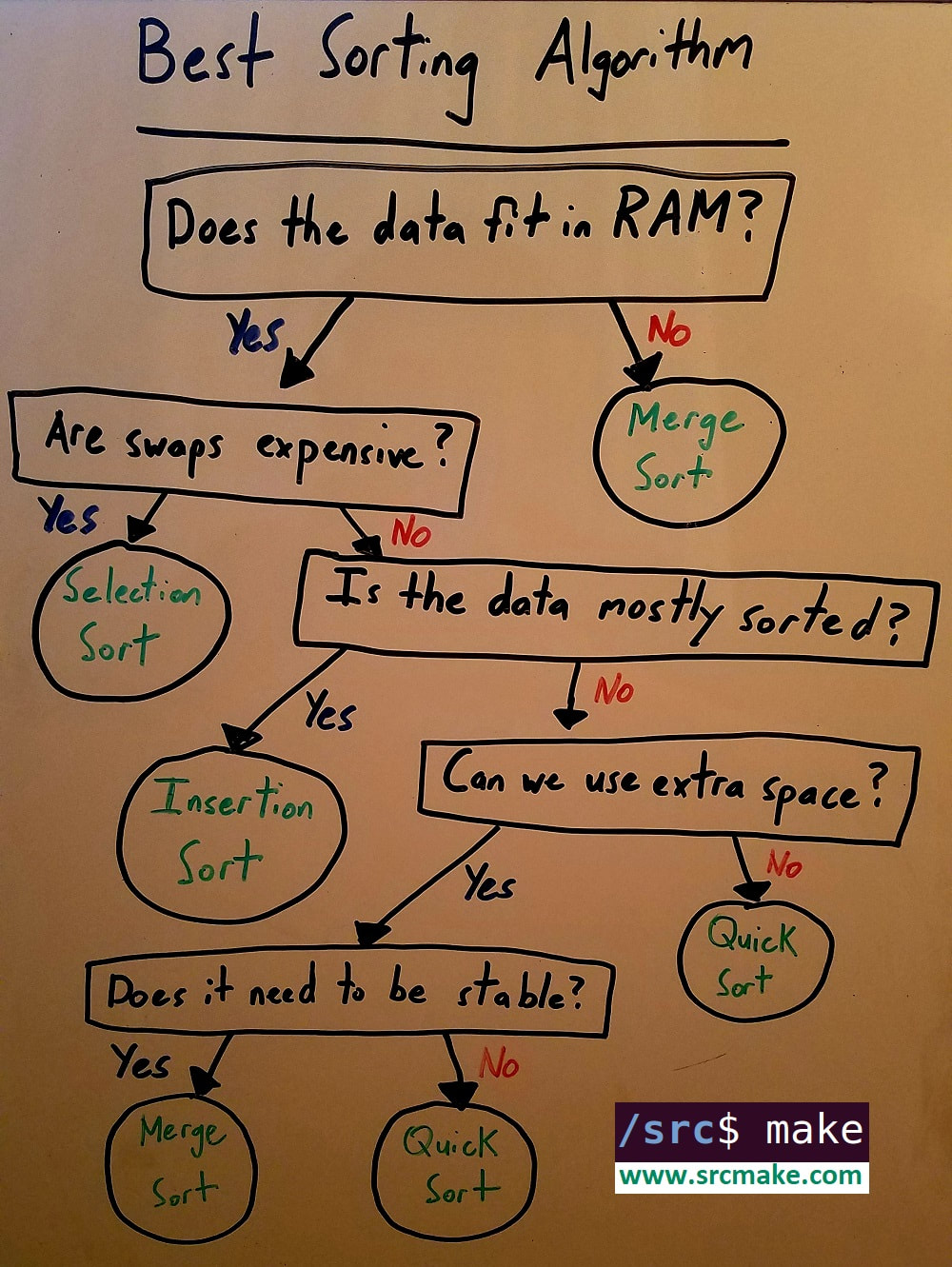
When To Use Each Sorting Algorithm (Decision Tree)

So here's how to decide which sorting algorithm to use (generally):

Note that this is a very good guideline (and probably good enough for an interview), but you should be aware that advanced techniques exist. For example, any sort can be made "stable", but sometimes it's not worth it. There's always trade-offs.

Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
Github: srcmake

References
1. Programming Interviews Exposed by Eric Giguere, John Mongan, Noah Suojanen.
2. geekforgeeks Selection Sort.
3. geekforgeeks Insertion Sort.
4. geekforgeeks Merge Sort.
5. geekforgeeks Quick Sort.