[Interview Question] Zombies In A Matrix (Also On Leetcode)

To watch the youtube video going over this topic, please click here.

Problem Statement

A matrix (2D array) has cells that are filled with one of three possible values:

• The cell is empty (0)
• The cell has a human in it (1)
• The cell has a zombie in it (2)

Every turn, the zombies infect any humans adjacent to them  (up/down/left/right), and those humans become zombies. Those new zombies are then able to infect any humans next to then, and the cycle continues each turn.

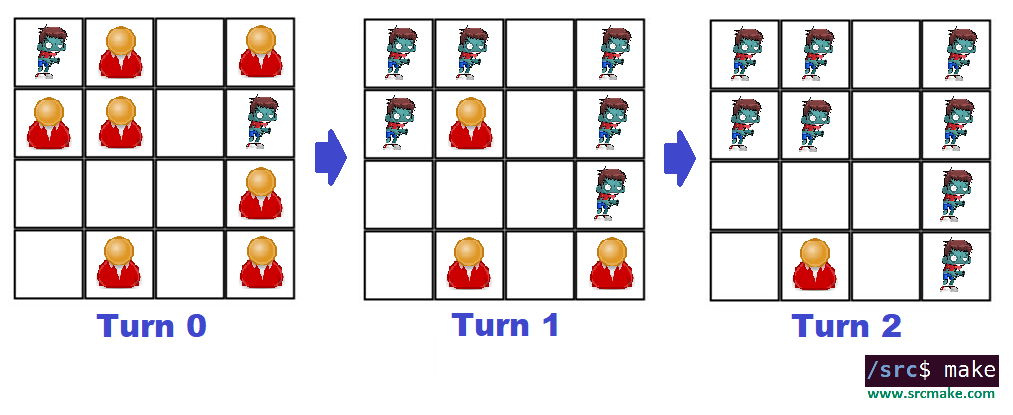
​Given a matrix, to return the number of turns it takes until there are no humans left. (And if any human survives, then return -1.) ​("Rotting Oranges" problem on Leetcode.)

The zombies in a matrix problem. Each turn, zombies infect any humans adjacent to them, and those humans become zombies.

---

Solution (Multiple BFS)

Theory
The way we'll solve this problem is by updating the matrix each turn by infecting humans next to any zombies.

​However, there are two things we need to watch out for:

1. We must infect humans on the correct turns.
2. We don't want to traverse empty cells unnecessarily.

With this in mind, we'll use a queue to hold each zombie, and for each zombie in the queue we'll process it by allowing it to infect any humans adjacent too it (meaning pushing that newly created zombie onto the queue to be processed later).

However, the part where our code is going to become easier to read (and differs from the Leetcode solution) is that each Zombie in our queue will store their matrix position (i,j) and the turn it got infected. To do this, we'll have a special data structure (a struct or a class) to store this extra info.

Algorithm

• Create a struct/class named Zombie that stores integers i, j, and turnInfected.
• Create a queue that holds Zombies. 
• Traverse the matrix and if we see a zombie, add it to the queue (where turnInfected = 0).
• For each zombie in the queue...
  • Update the current turn to be this zombie's turnInfected.
  • Infect any humans next to this zombie (and add those new zombies to the queue).
• Now that all zombification is done, traverse the matrix to check if any humans survived.
• If any humans survived, return -1. Otherwise return the current turn.

C++ Code

​Analysis
The time complexity is O(N), where N is the number of cells in the matrix, since we'll process each cell at most once. 

The space complexity is O(N), since at worst the queue holds all zombies. (Meaning we start out with a matrix full of zombies and they all get pushed into the queue.)

Note: This solution is called "multiple BFS" because we're using a queue to traverse nodes (zombies) like the BFS algorithm, but we've got multiple nodes (zombies) being traversed at the same time. 

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake