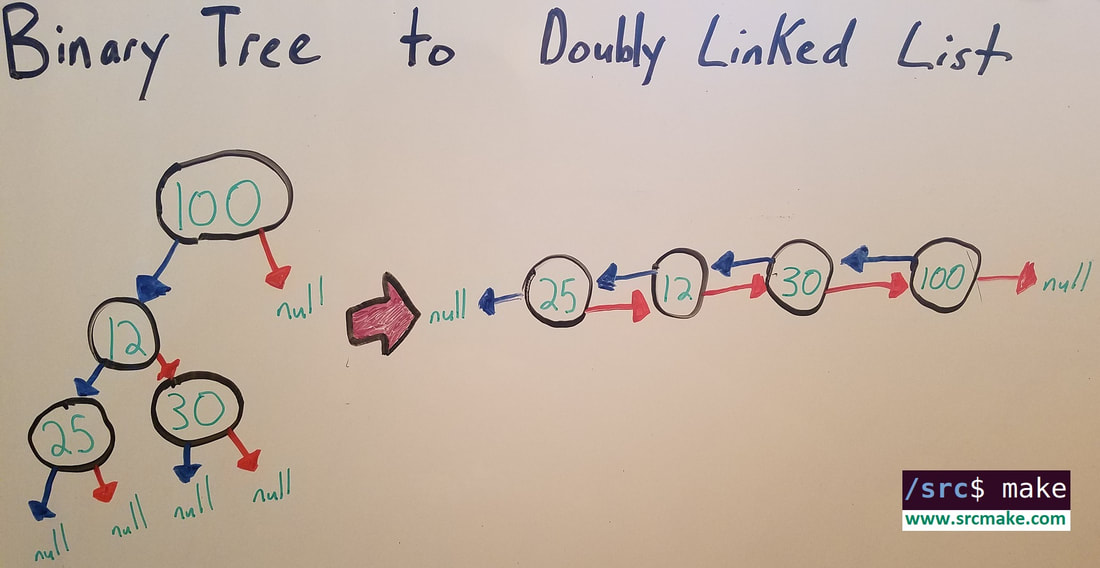Interview: Converting A Binary Tree To A Doubly Linked List (C++ Code)

Intro - Binary Trees and Doubly Linked Lists

A popular interview question is converting a Binary Tree to a Doubly Linked List. 

A Binary Tree (BT) is a hierachical graph data structure. Here's a blog post on Trees if you've never seen one before. (Note: We don't care if it's a Binary Search Tree, it just needs to be a binary tree.)

A Doubly Linked List is a data structure where nodes that hold information are sequentially chained: each node holds a pointer to the next node in the chain. Here's a blog post on Linked Lists if you're new to them.

A binary tree (notice it's not a BST) gets converted to a doubly linked list.

BST To Doubly Linked List: Our Algorithm

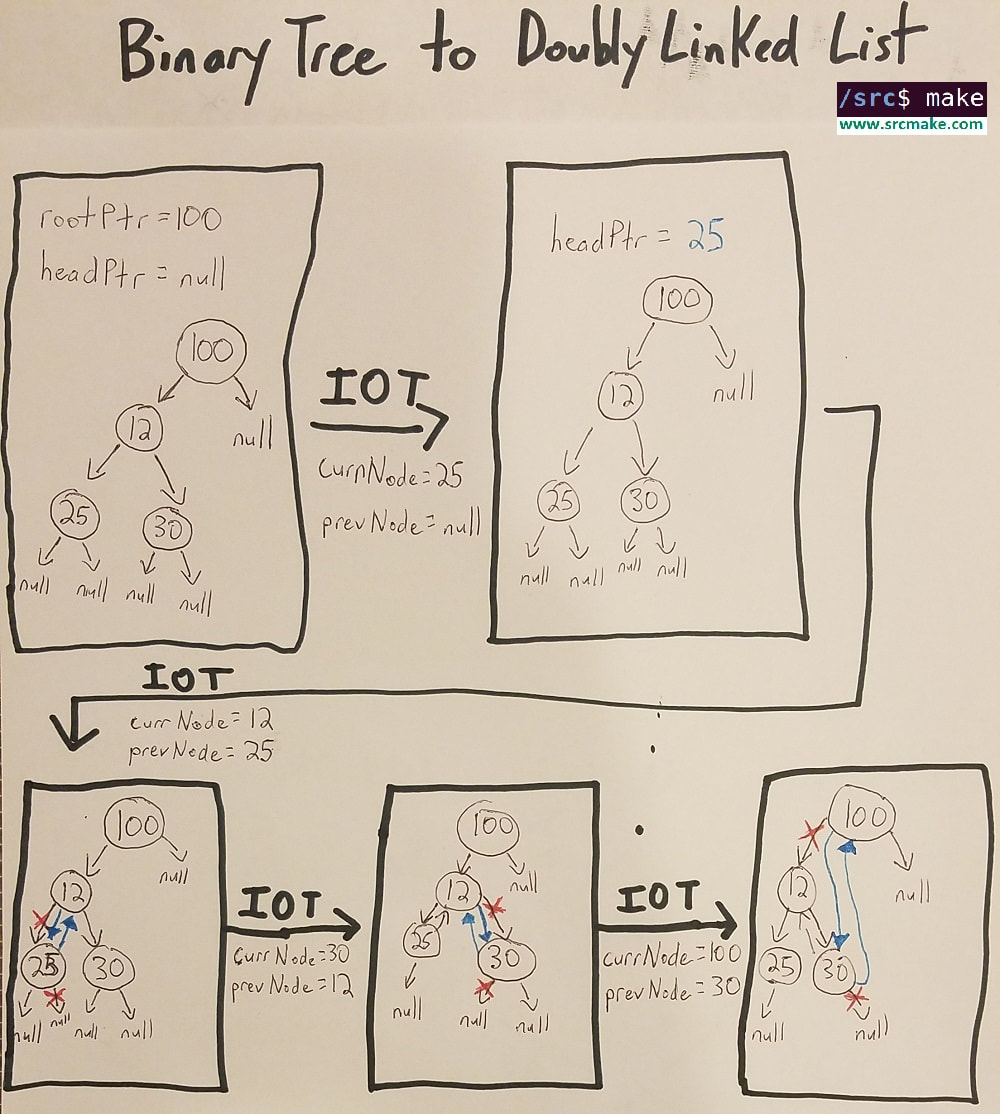
Our algorithm to convert a Binary Tree to a Double Linked List is pretty simple. We'll do an In-Order Traversal of the tree (which ends up visiting the nodes in the order: 25 12 30 100 (which is the order we want our DLL to be), and we'll keep track of the current node that we're looking at, and the previous node that we've visited. 

At each step, we'll make the currentNode's left pointer point to the previousNode, and we'll make the previousNode's right pointer point to the currentNode. Simple, right?

(We'll also cover one specific case where our first node becomes the "prevNode", and we have a head pointer for our linked list point to that node.)

​See the diagram below to see how this works.

Step by Step how the algorithm works, on a simple example.

The Code (In C++)

Our code will implement the algorithm described above as one In-Order Traversal recursive function. I've also borrowed some code from previous blog posts to create/add nodes to a binary tree, and to print a linked list, so view those blog posts if you want too.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128

// Copyright srcmake.com 2018. // C++ Binary Tree To Doubly Linked List Code // Official webpage for this tutorial: https://www.srcmake.com/home/bt2dll /* Compile with: g++ -std=c++14 main.cpp -o run ./run */ #include <iostream> using namespace std; ////////////////////////////////////////////////////// ////// BINARY TREE STUFF ////// // Copying and pasting some tree code from https://www.srcmake.com/home/trees // Our node. struct node { int data; // The data struct node* left; // A pointer to the node for the left child. struct node* right; // A pointer to the node for the right child. node(int data) { this->data = data; this->left = NULL; this->right = NULL; } }; ///////////////////////////////////////////////////// ////////////////////////////////////////////////////// ////// LINKED LIST STUFF ////// // Copying and pasting some linked list code from https://www.srcmake.com/home/linkedlist // Print all nodes in the list. void PrintLinkedList(node* nodePtr) { // If this node is null, stop. if(nodePtr == NULL) { cout << endl; return; } // Print this node's data. cout << nodePtr->data << " "; // Recursively check the next node in the list. PrintLinkedList(nodePtr->right); } ////////////////////////////////////////////////////// ////////////////////////////////////////////////////// ////// BINARY TREE TO DOUBLY LINKED LIST ////// // Convert a binary tree to a doubly linked list in-place. O(1) space, O(N) time. // Do an In-Order-Traversal and change left and right pointers of each node. // @currNode is the node we're currently looking at. // @prevNode is a reference (we need the value to be known to all recursive calls) to the last node we visited. // @headPtr is a reference to the head of the linked list. (We only update this once.) void BT2DLL(node* currNode, node*& prevNode, node*& headPtr) { /// Base case: Node doesn't exist. if(currNode == NULL) { return; } /// Left BT2DLL(currNode->left, prevNode, headPtr); /// Current Node // If this is the first node in the list... if(prevNode == NULL) { // Set the head pointer to point to this node. headPtr = currNode; // Update the prevNode to be this one. prevNode = currNode; } // Otherwise, this isn't the first node in the list. else { // Make the currentNode's left pointer point to the prevNode. currNode->left = prevNode; // Make the prevNode's right pointer point to the currNode. prevNode->right = currNode; // Update the prevNode to be this one. prevNode = currNode; } /// Right BT2DLL(currNode->right, prevNode, headPtr); } ////////////////////////////////////////////////////// ////////////////////////////////////////////////////// ////// MAIN ////// int main() { cout << "Program started.\n"; // First, create our binary tree. node* root = new node(100); root->left = new node(12); root->left->left = new node(25); root->left->right = new node(30); // Create a pointer for the head of our linked list. // (Initially it's null.) node* headPtr = NULL; // The previous node that we visited doesn't exist yet. node* prevNode = NULL; // Now call BT2DLL. BT2DLL(root, prevNode, headPtr); // Print the new linked list. PrintLinkedList(headPtr); cout << "Program ended.\n"; return 0; } //////////////////////////////////////////////////////

The time complexity is O(N), as we visit each node exactly once, and the space complexity is O(1), since we use no extra space (since we don't create new nodes, we just update the pointers).

Conclusion

This is a popular interview question, and tests your knowledge of two fundamental data structured (binary trees and linked lists), as well as your recursive and pointer (and reference) skill, so make sure you can write this code yourself.

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake

References:
1. Geekforfeeks.