Trees - Regular, Binary, Binary Search, Traversal (with C++ Code)

Trees - A Fundamental Data Structure

Trees are a specific type of graph data structure. (You can see another blog post explaining C++ graphs here.)

A tree is a hierarchy of nodes, where each node stores some information, along with pointers to other nodes in the tree. Specifically, nodes (vertices) connect to each other with edges. The top node of the tree is called the "root".

A tree data structure. The nodes are in a hierarchy.

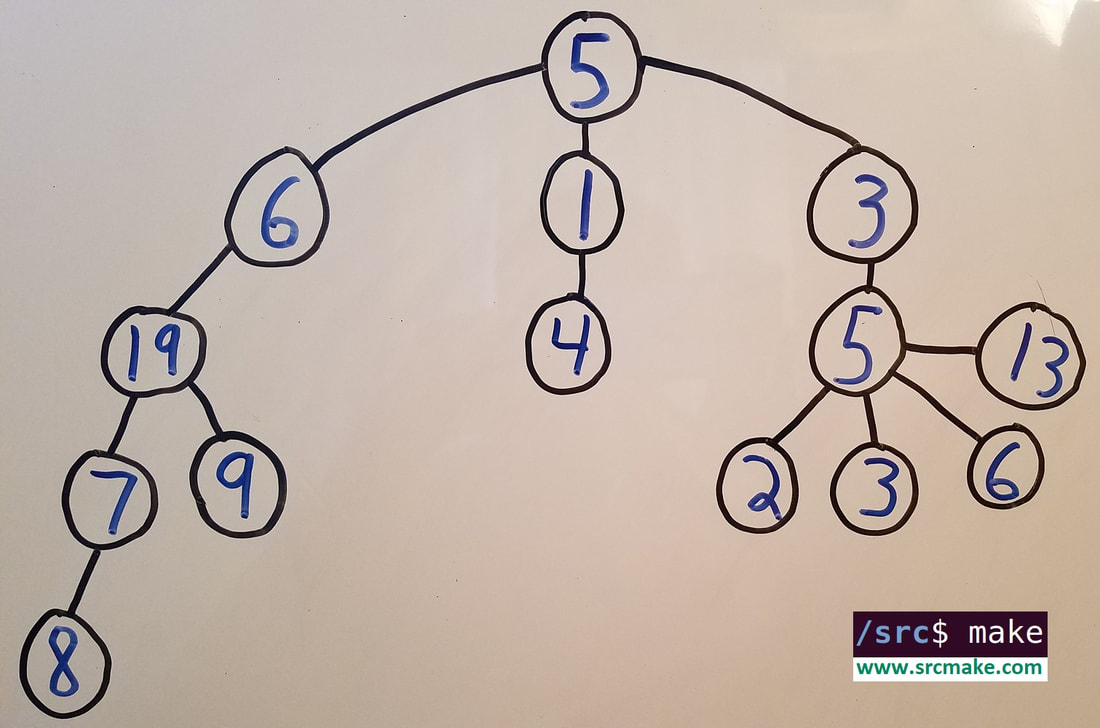
A good way to check if a tree is a tree is "if all the tree's edges are drawn with straight lines, none of the lines must overlap". If the lines aren't straight or if they do overlap, then it's not really a "tree" because there wouldn't be a proper hierarchy.

Binary Trees

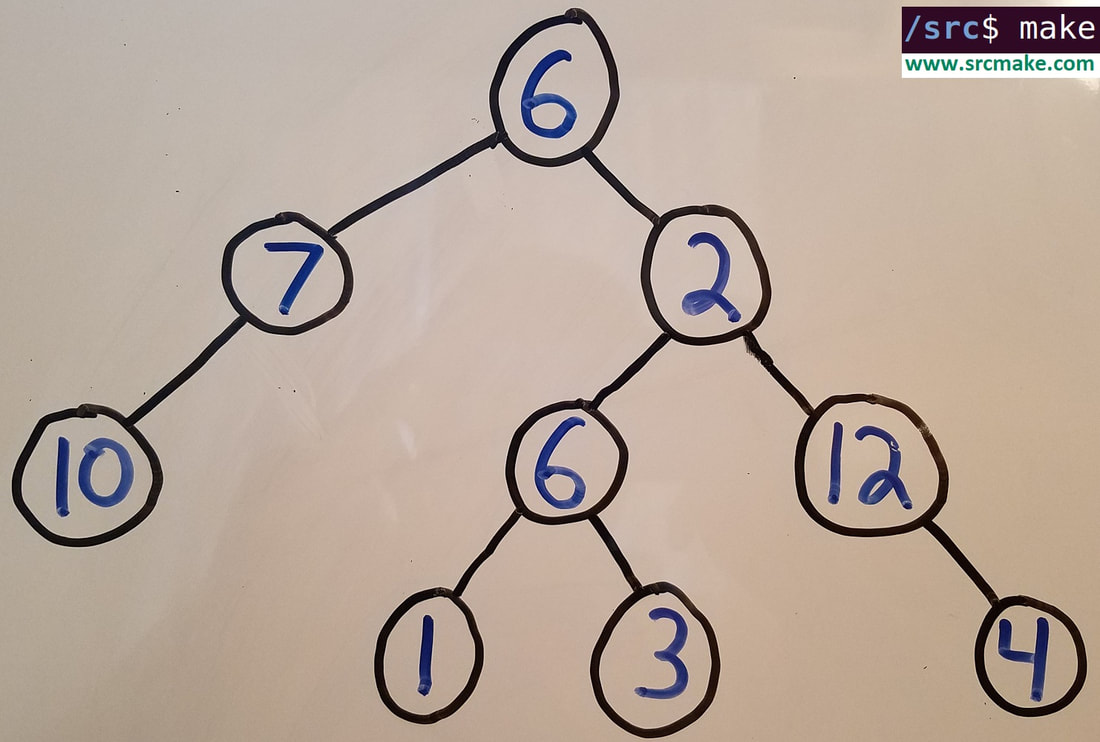
Binary Trees are special trees. All nodes in the tree have at most two child nodes (usually labeled as "left" or "right").

A binary tree. Each node has 0, 1, or 2 children.

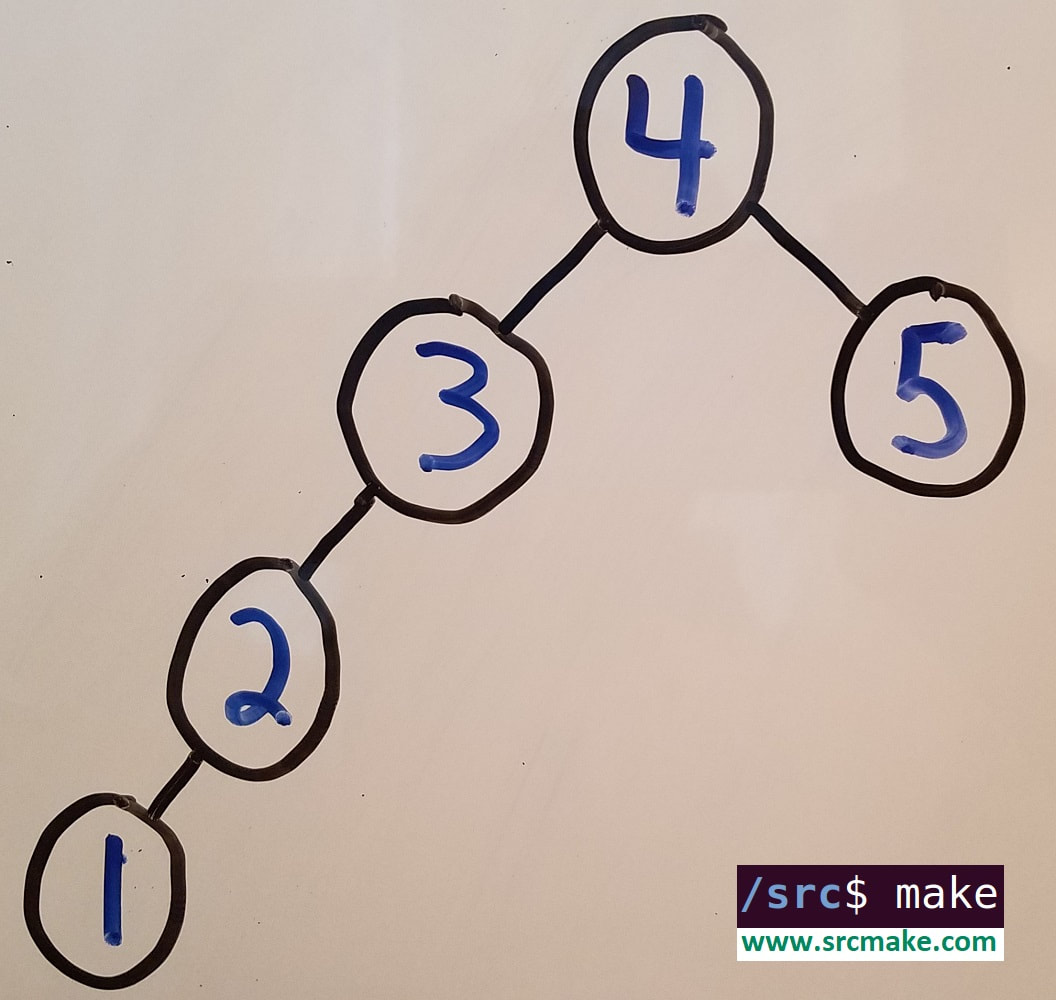
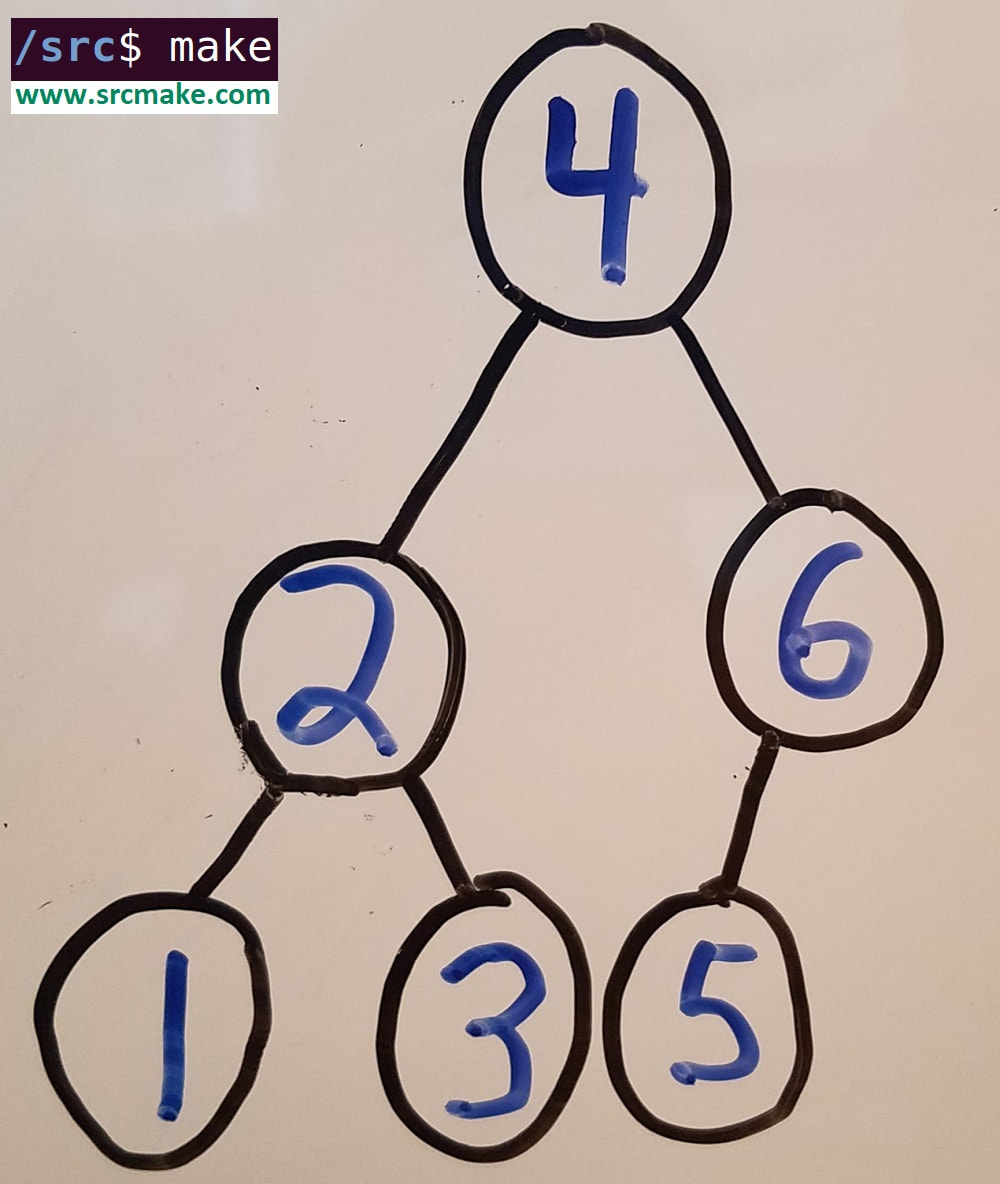
Binary Search Trees

Binary Search Trees are special types of Binary Trees. In a BST, all "left" child nodes are smaller than their parents, and all "right" child nodes are larger than their parents. A BST can be considered a sorted binary tree.

There should be no duplicate keys (the value in a node which used to determine "smaller" or "larger" nodes) in the tree: each key should be unique.

A binary search tree. Each node's left child (and it's children) are smaller than it, and each node's right child (and all it's children) are bigger than it.

Perfect Binary Search Trees

A perfect binary search tree (or a "balanced" binary tree) is one where, no matter which path of the tree you go down, the difference between "leaves" (a "leaf" is a child node at the bottom of the tree, with no children) is at most one.

Perfect BSTs are very important in computer science because it's a data structure that allows us to access data in log-base2(n) time, which is very useful compared to basic data structures like arrays or linked lists.

A balanced/perfect BST. All leaf nodes have a height difference of 0 or 1 with each other.

Binary Tree C++ Code

Let's look at how a binary tree is represented in C++. A node is just a structure that has three (or more) variables inside of it: a pointer to a left child, a pointer to a right child, and the actual data that we care about storing.

// Copyright srcmake.com 2018.
// C++ Tree Code
// C++ Preorder, Inorder, and Postorder Traversal
// Official webpage for this tutorial: https://www.srcmake.com/home/trees

/* Compile with:
g++ -std=c++14 main.cpp -o run
./run
*/

#include <iostream>
using namespace std;

//////////////////////////////////////////////////////
/////// NODE ///////
// This struct represents the node in our tree.
struct node
    {
    int value;            // The value 
    struct node* left;    // A pointer to the node for the left child.
    struct node* right;    // A pointer to the node for the right child.
    
    //////////////////////
    // THESE CONSTRUCTORS ARE OPTIONAL. We'll see it used in node2.
    // This constructor will make initializing a node easier.
    node(int value)
        {
        this->value = value;
        this->left = NULL;
        this->right = NULL;
        }
        
    // Create a blank constructor so that we don't need to initialize a node
    // with the value if we don't want too.
    node()
        {
        }
    //////////////////////
    };
/////////////////////////////////////////////////////

//////////////////////////////////////////////////////
////// MAIN //////
int main() 
    {
    cout << "Program started.\n";
    
    // Create the root.
    node root;
    root.value = 5;
    root.left = NULL;
    root.right = NULL;
    
    // Create another node.
    node node1;
    node1.value = 2;
    node1.left = NULL;
    node1.right = NULL;
    
    // Make node1 the left child of root.
    // (By making root's left child point to the address of node1.)
    root.left = &node1;
    
    // Verify that this works by printing root's left child's value.
    cout << root.left->value << endl;
    // (The syntax is like that because root.left is really "struct node* left"
    // so we access the value of that pointer by using the -> operator.)
    
    // Create another node. Let's use the constructor this time.
    // Add this node directly as the root's right child.
    root.right = new node(10);
    
    // Verify that this works by printing root's left child's value.
    cout << root.right->value << endl;
    
    cout << "Program ended.\n";
    return 0;
    }
//////////////////////////////////////////////////////

(Notice the difference in syntax between the . and -> operators. If we have a variable that actually represents a a node (like node root;) then we use the . operator, but when talking about a pointer to a node, we use the
-> operator.)

Tree Traversal

Okay, so we can create a tree, but how do we actually use it? Tree traversal is typically done using recursion, and there are three types of traversals that matter.

Pre-Order Traversal - Node -> Left Child -> Right Child. This is like a Depth-First-Search which checks left children first.
In-Order Traversal - Left Child -> Node -> Right Child. This will yield the sorted list of the items in the array. It starts at the bottom left of the tree and finished at the bottom right.
Post-Order Traversal - Left Child -> Right Child -> Node.

Remembering these three traversal types will help when writing a recursive function, since it dictates the placement in the function's code.

Tree Traversal C++ Code

The following code demonstrates tree traversal techniques. Simply create the tree, and pass the root of the tree to functions to print the traversed nodes.

// Copyright srcmake.com 2018.
// C++ Tree Code
// C++ Preorder, Inorder, and Postorder Traversal
// Official webpage for this tutorial: https://www.srcmake.com/home/trees

/* Compile with:
g++ -std=c++14 main.cpp -o run
./run
*/

#include <iostream>
using namespace std;

//////////////////////////////////////////////////////
/////// NODE ///////
// This struct represents the node in our tree.
struct node
    {
    int value;            // The value 
    struct node* left;    // A pointer to the node for the left child.
    struct node* right;    // A pointer to the node for the right child.
    
    // Constructor
    node(int value)
        {
        this->value = value;
        this->left = NULL;
        this->right = NULL;
        }
    };
/////////////////////////////////////////////////////


/////////////////////////////////////////////////////
////// PREORDER TRAVERSAL //////
// Print the nodes, going in preorder traversal.
// The function is passed a pointer of a node in the tree.
void PrintPreorderTraversal(node* node)
    {
    // If the pointer points to null instead of an actual node, stop.
    if(node == NULL)
        { return; }
    
    // Node.
    cout << node->value << " ";
    
    // Left.
    PrintPreorderTraversal(node->left);
    
    // Right.
    PrintPreorderTraversal(node->right);
    }
/////////////////////////////////////////////////////


/////////////////////////////////////////////////////
////// INORDER TRAVERSAL //////
// Print the nodes, going in inorder traversal.
// The function is passed a pointer of a node in the tree.
void PrintInorderTraversal(node* node)
    {
    // If the pointer points to null instead of an actual node, stop.
    if(node == NULL)
        { return; }
    
    // Left.
    PrintInorderTraversal(node->left);
    
    // Node.
    cout << node->value << " ";
    
    // Right.
    PrintInorderTraversal(node->right);
    }
/////////////////////////////////////////////////////


/////////////////////////////////////////////////////
////// POSTORDER TRAVERSAL //////
// Print the nodes, going in postorder traversal.
// The function is passed a pointer of a node in the tree.
void PrintPostorderTraversal(node* node)
    {
    // If the pointer points to null instead of an actual node, stop.
    if(node == NULL)
        { return; }
    
    // Left.
    PrintPostorderTraversal(node->left);
    
    // Right.
    PrintPostorderTraversal(node->right);
    
    // Node.
    cout << node->value << " ";
    }
/////////////////////////////////////////////////////


//////////////////////////////////////////////////////
////// MAIN //////
int main() 
    {
    cout << "Program started.\n";
    
    // Create a new node and have a pointer to it, which we'll call root.
    node* root = new node(4);
    
    // Add the rest of the nodes of the tree.
    root->left = new node(2);
    root->right = new node(6);
    root->left->left = new node(1);
    root->left->right = new node(3);
    root->right->left = new node(5);
    
    // Pass the root node to the traversal functions.
    cout << "Preorder Traversal: ";
    PrintPreorderTraversal(root);
    cout << endl;
    
    cout << "Inorder Traversal: ";
    PrintInorderTraversal(root);
    cout << endl;
    
    cout << "Postorder Traversal: ";
    PrintPostorderTraversal(root);
    cout << endl;
    
    cout << "Program ended.\n";
    return 0;
    }
//////////////////////////////////////////////////////

Conclusion

With this fundamental tree knowledge, we can look to more advanced questions (since trees are popular in interviews).

In future tutorials, we'll look at some tree interview questions that have to do with special traversal or placement of items in the tree. In another tutorial, we'll look at advanced tree data structures and concepts, such as balancing a Binary Tree so that it can become a BST, or looking at how red-black trees work.

Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
Github: srcmake

References
1. medium.freecodecamp.org/all-you-need-to-know-about-tree-data-structures-bceacb85490c
2. https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/