Powered by
/src$ make
  • Home
  • About
  • Directory
  • Contact
  • Home
  • About
  • Directory
  • Contact

C++ Shortest Path - Dijkstra PQ Implementation, Bellman-Ford Code As Backup, and Floyd Warshall

4/5/2018

 

Introduction: Shortest Paths

We've already had a blog post on graph theory, adjacency lists/matrixes for representing a graph, and BFS/DFS for traversing a graph. So how do we find the shortest path in a graph if there are edge weights? The answer is...we use the famous Dijkstra algorithm. (Assuming there are no negative edge weights.) If there are negative edge weights, then we use Bellman Ford. 

What we want is, for a starting vertex/node, a list containing the shortest path from the starting node to every other node. 
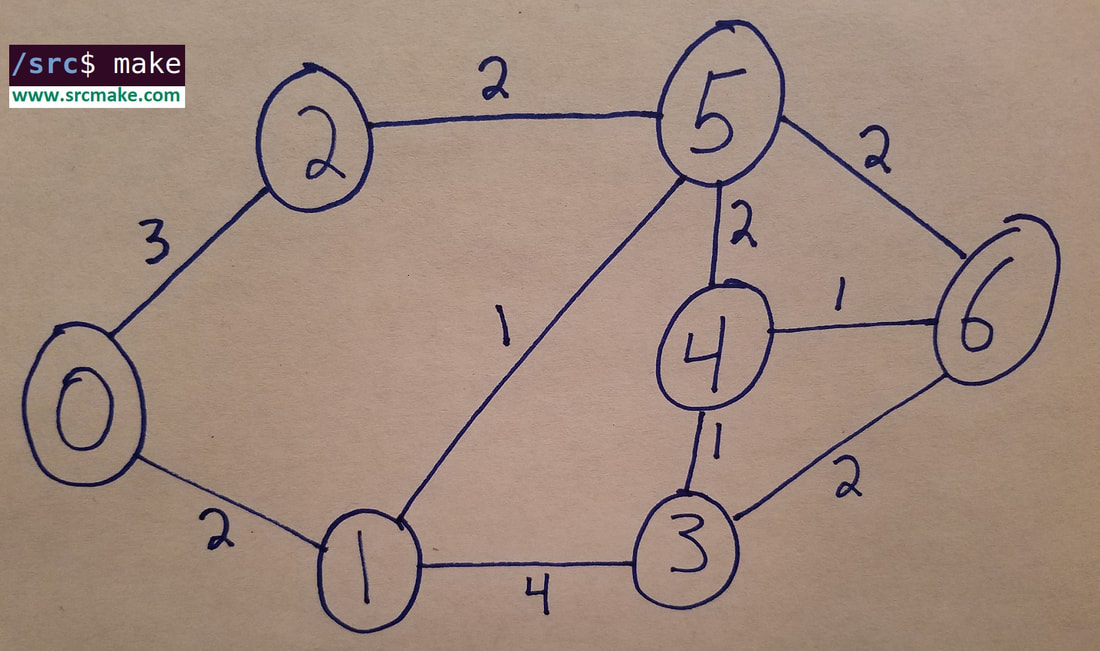
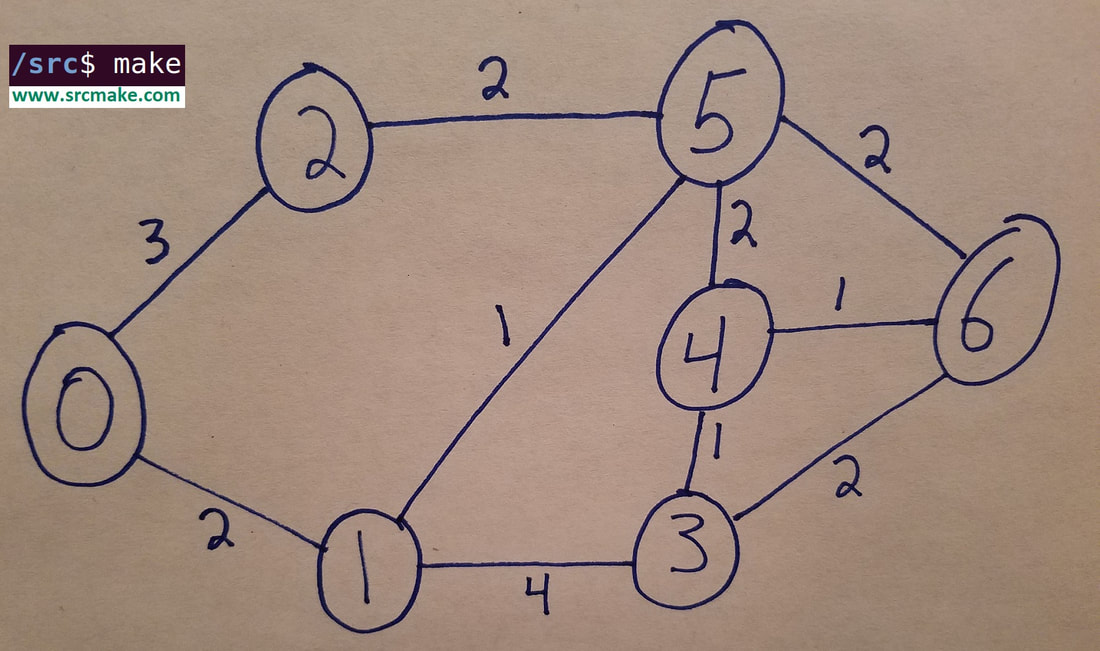
Picture
Picture
The above graph is what we'll be using in our algorithms. You can see that there are some nodes (vertices) labeled 0 to 6, and there are some edges that each have weights on them. We want the shortest path (lowest weight total) from one node to another. To the right is the adjacency list representation of the graph, where for adjList[i], there's a vector of pair<int, int>s at each index, where the first int represents the neighbor node, and the second int represents the edge weight between them.

Djikstra's Algorithm For Shortest Paths, using Priority Queue

Djikstra's algorithm is going to maintain a list of shortest paths from the starting node to all other nodes. Initially, the starting node has 0 distance to itself, but infinity distance to all other nodes. Then, by looking at all neighbors, of the node we're processing (starting with the start node), we'll update the shortest distances by checking if we can do better.

In this implementation, we use a priority queue, which will prioritize checking the shortest edge weights first.
Our code will generate that adjacency list, and perform the algorithm we mentioned before.  
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

// Copyright srcmake.com 2018.
// C++ Example Dijkstra Algorithm For Shortest Path (With PQ/Min-Heap)

/* The Dijkstra algorithm:
    // Initialize the graph adjacency list. adjList[i] = pair<int, int> where first is vertex, second is edge weight.
    // Initialize all source->vertex as infinite.
    // Create a PQ.
    // Add source to pq, where distance is 0.
    // While pq isn't empty...
        // Get min distance vertex from pq. (Call it u.)
        // Visit all of u's friends. For each one (called v)....
            // If the distance to v is shorter by going through u...
                // Update the distance of v.
                // Insert v into the pq. 
*/

// The example graph: https://www.srcmake.com/uploads/5/3/9/0/5390645/spgraph_orig.jpg

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// An adjacency list. Each adjList[i] holds a all the friends of node i.
// The first int is the vertex of the friend, the second int is the edge weight.
vector< vector<pair<int, int> > > FormAdjList()
    {
    // Our adjacency list.
    vector< vector<pair<int, int> > > adjList;
    
    // We have 7 vertices, so initialize 7 rows.
    const int n = 7;
    
    for(int i = 0; i < n; i++)
        {
        // Create a vector to represent a row, and add it to the adjList.
        vector<pair<int, int> > row;
        adjList.push_back(row);
        }
    
    
    // Now let's add our actual edges into the adjacency list.
    // See the picture here: https://www.srcmake.com/uploads/5/3/9/0/5390645/spadjlist_orig.jpg
    
    adjList[0].push_back(make_pair(1, 2));
    adjList[0].push_back(make_pair(2, 3));
    
    adjList[1].push_back(make_pair(0, 2));
    adjList[1].push_back(make_pair(5, 1));
    
    adjList[2].push_back(make_pair(0, 3));
    adjList[2].push_back(make_pair(5, 2));
    
    adjList[3].push_back(make_pair(1, 4));
    adjList[3].push_back(make_pair(4, 1));
    adjList[3].push_back(make_pair(6, 2));
    
    adjList[4].push_back(make_pair(3, 1));
    adjList[4].push_back(make_pair(5, 2));
    adjList[4].push_back(make_pair(6, 1));
    
    adjList[5].push_back(make_pair(1, 1));
    adjList[5].push_back(make_pair(2, 2));
    adjList[5].push_back(make_pair(4, 2));
    adjList[5].push_back(make_pair(6, 2));
    
    adjList[6].push_back(make_pair(3, 2));
    adjList[6].push_back(make_pair(4, 1));
    adjList[6].push_back(make_pair(5, 2));
    
    // Our graph is now represented as an adjacency list. Return it.
    return adjList;
    }
    
// Given an Adjacency List, find all shortest paths from "start" to all other vertices.
vector<int> DijkstraSP(vector< vector<pair<int, int> > > &adjList, int &start)
    {
    cout << "\nGetting the shortest path from " << start << " to all other nodes.\n";
    vector<int> dist;
    
    // Initialize all source->vertex as infinite.
    int n = adjList.size();
    for(int i = 0; i < n; i++)
        {
        dist.push_back(1000000007); // Define "infinity" as necessary by constraints.
        }
        
    // Create a PQ.
    priority_queue<pair<int, int>, vector< pair<int, int> >, greater<pair<int, int> > > pq;
    
    // Add source to pq, where distance is 0.
    pq.push(make_pair(start, 0));
    dist[start] = 0;
    
    // While pq isn't empty...
    while(pq.empty() == false)
        {
        // Get min distance vertex from pq. (Call it u.)
        int u = pq.top().first;
        pq.pop();
        
        // Visit all of u's friends. For each one (called v)....
        for(int i = 0; i < adjList[u].size(); i++)
            {
            int v = adjList[u][i].first;
            int weight = adjList[u][i].second;
            
            // If the distance to v is shorter by going through u...
            if(dist[v] > dist[u] + weight)
                {
                // Update the distance of v.
                dist[v] = dist[u] + weight;
                // Insert v into the pq. 
                pq.push(make_pair(v, dist[v]));
                }
            }
        }
    
    return dist;
    }
    
void PrintShortestPath(vector<int> &dist, int &start)
    {
    cout << "\nPrinting the shortest paths for node " << start << ".\n";
    for(int i = 0; i < dist.size(); i++)
        {
        cout << "The distance from node " << start << " to node " << i << " is: " << dist[i] << endl;
        }
    }
    
int main() 
    {
    cout << "Program started.\n";
    
    // Construct the adjacency list that represents our graph. 
    vector< vector<pair<int, int> > > adjList = FormAdjList();
    
    // Get a list of shortest path distances for node 0.
    int node = 0;
    vector<int> dist = DijkstraSP(adjList, node);
    
    // Print the list.
    PrintShortestPath(dist, node);
    
    cout << "Program ended.\n";
    
    return 0;
    }

Bellman-Ford - Good For Negative Edges

Dijkstra is a greedy algorithm and will fail if there are cycles or negative edge weights. Because of this, we need the Bellman-Ford algorithm in that case. (But it's slower than Dijkstra, so use Dijkstra depending on the problem constraints.)  
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155

// Copyright srcmake.com 2018.
// C++ Bellman-Ford Algorithm For Shortest Path
/* Use it if there are negative edge weights in a graph. */

/* Algorithm: 
    // Create the adjacency list that represents the graph. 
    // Initialize a list for the distances from source to each other node as infinity. (Source to itself is 0.)
    // Then calculate the shortest distance using...
    // For numNodes-1...
        // For each node (u)...
            // For each of it's neighbors (v)...
                // If the distance from source to v is bigger than dist[u] + weight of (u,v)...
                    // Update dist[v] to dist[u] + weight(u,V)
                    
    // If there's a negative weight cycle in the graph, then report it, by...
    // For each node (u)...
        // For each of u's neighbors (v)...
            // Check if it's possible to get even better (now, that we should be at shortest)
            // If the distance from source to v is bigger than dist[u] + weight of (u,v)...
                // Report problem.
*/

// The example graph: https://www.srcmake.com/uploads/5/3/9/0/5390645/spgraph_orig.jpg

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// An adjacency list. Each adjList[i] holds a all the friends of node i.
// The first int is the vertex of the friend, the second int is the edge weight.
vector< vector<pair<int, int> > > FormAdjList()
    {
    // Our adjacency list.
    vector< vector<pair<int, int> > > adjList;
    
    // We have 7 vertices, so initialize 7 rows.
    const int n = 7;
    
    for(int i = 0; i < n; i++)
        {
        // Create a vector to represent a row, and add it to the adjList.
        vector<pair<int, int> > row;
        adjList.push_back(row);
        }
    
    
    // Now let's add our actual edges into the adjacency list.
    // See the picture here: https://www.srcmake.com/uploads/5/3/9/0/5390645/spadjlist_orig.jpg
    
    adjList[0].push_back(make_pair(1, 2));
    adjList[0].push_back(make_pair(2, 3));
    
    adjList[1].push_back(make_pair(0, 2));
    adjList[1].push_back(make_pair(5, 1));
    
    adjList[2].push_back(make_pair(0, 3));
    adjList[2].push_back(make_pair(5, 2));
    
    adjList[3].push_back(make_pair(1, 4));
    adjList[3].push_back(make_pair(4, 1));
    adjList[3].push_back(make_pair(6, 2));
    
    adjList[4].push_back(make_pair(3, 1));
    adjList[4].push_back(make_pair(5, 2));
    adjList[4].push_back(make_pair(6, 1));
    
    adjList[5].push_back(make_pair(1, 1));
    adjList[5].push_back(make_pair(2, 2));
    adjList[5].push_back(make_pair(4, 2));
    adjList[5].push_back(make_pair(6, 2));
    
    adjList[6].push_back(make_pair(3, 2));
    adjList[6].push_back(make_pair(4, 1));
    adjList[6].push_back(make_pair(5, 2));
    
    // Our graph is now represented as an adjacency list. Return it.
    return adjList;
    }
    
// Given an Adjacency List, find all shortest paths from "start" to all other vertices.
vector<int> BellmanFordSP(vector< vector<pair<int, int> > > &adjList, int &start)
    {
    cout << "\nGetting the shortest path from " << start << " to all other nodes.\n";
    vector<int> dist;
    
    // Initialize all source->vertex as infinite.
    int n = adjList.size();
    for(int i = 0; i < n; i++)
        {
        dist.push_back(1000000007); // Define "infinity" as necessary by constraints.
        }
        
    dist[start] = 0;    
    
    // Then calculate the shortest distance using...
    // For numNodes-1...
    for(int i = 0; i < n-1; i++)
        {
        // For each node (u)...
        for(int u = 0; u < n; u++)
            {
            // For each of it's neighbors (v)...
            for(int j = 0; j < adjList[u].size(); j++)
                {
                int v = adjList[u][j].first;
                int weight = adjList[u][j].second;
                
                // If the distance from source to v is bigger than dist[u] + weight of (u,v)...
                if(dist[v] > dist[u] + weight)
                    {
                    // Update dist[v] to dist[u] + weight(u,V)
                    dist[v] = dist[u] + weight;
                    }
                }
            }
        }            
    // If there's a negative weight cycle in the graph, then report it, by...
    // For each node (u)...
        // For each of u's neighbors (v)...
            // Check if it's possible to get even better (now, that we should be at shortest)
            // If the distance from source to v is bigger than dist[u] + weight of (u,v)...
                // Report problem.
    
    return dist;
    }
    
void PrintShortestPath(vector<int> &dist, int &start)
    {
    cout << "\nPrinting the shortest paths for node " << start << ".\n";
    for(int i = 0; i < dist.size(); i++)
        {
        cout << "The distance from node " << start << " to node " << i << " is: " << dist[i] << endl;
        }
    }
    
int main() 
    {
    cout << "Program started.\n";
    
    // Construct the adjacency list that represents our graph. 
    vector< vector<pair<int, int> > > adjList = FormAdjList();
    
    // Get a list of shortest path distances for node 0.
    int node = 0;
    vector<int> dist = BellmanFordSP(adjList, node);
    
    // Print the list.
    PrintShortestPath(dist, node);
    
    cout << "Program ended.\n";
    
    return 0;
    }
The results of running this should be exactly the same as Dijkstra. (But this takes longer.)

Floyd Warshall - Efficient For All Sources To All Nodes

Dijkstra and Bellman-Ford calculate the shortest path in a graph from one source node to all other nodes. But what if we need to calculate the shortest distance from all sources as the starting node, to all other nodes? That's what the Floyd Warshall algorithm is for.
We'll need an adjacency matrix representation of our graph for this problem. This time, edge weights that don't exist are set to infinity, and the distance of a node from itself is 0.
Picture
Picture 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163

// Copyright srcmake.com 2018.
// C++ Example Floyd Warshall Algorithm For Shortest Path
// Official webpage for this tutorial: https://www.srcmake.com/home/cpp-shortest-path-dijkstra

/* The Floyd Warshall algorithm:
    // Create an adjacency matrix to represent the graph. 
    // Initialize a solution matrix that's the same as the adjacency matrix.
    // For each vertex w...
        // For each vertex as source (named u).
            // For each vertex as destination (named v).
                // If vertex w is on the shortest path from u to v...
                // Update value of dist[u][v]
*/

// The example graph: https://www.srcmake.com/uploads/5/3/9/0/5390645/spgraph_orig.jpg

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

//////////////////////////////////////////////////////////////////////////////////////
// Create an adjacency matrix for our graph. 
// Our target adjMatrix: https://www.srcmake.com/uploads/5/3/9/0/5390645/spadjlist_orig.jpg
vector< vector<int> > FormAdjMatrix()
    {
    // We could use an array for the adjMatrix if we knew the size, but it's safer to use a vector.
    vector< vector<int> > adjMatrix;
    
    // Initialize the adjMatrix so that all vertices can visit themselves.
    // (Basically, make an identity matrix.)
    const int n = 7;
    
    for(int i = 0; i < n; i++)
        {
        // Initialize the row.
        vector<int> row;
        adjMatrix.push_back(row);
        
        // Set the row to have all INFINITE's. (Except the vertex itself.)
        for(int j = 0; j < n; j++)
            {
            int value = 1000000007; // Infinite is 1E9 + 7 for us.
            
            if(i == j) 
                { value = 0; }
            
            adjMatrix[i].push_back(value);
            }
        }
    
    // Our matrix is set up, we just need to set up the edges (vertex connections).
    // See this image: https://www.srcmake.com/uploads/5/3/9/0/5390645/adjm_2_orig.png
    
    adjMatrix[0][1] = 2;
    adjMatrix[1][0] = 2;
    
    adjMatrix[0][2] = 3;
    adjMatrix[2][0] = 3;
    
    adjMatrix[1][3] = 4;
    adjMatrix[3][1] = 4;
    
    adjMatrix[1][5] = 1;
    adjMatrix[5][1] = 1;
    
    adjMatrix[2][5] = 2;
    adjMatrix[5][2] = 2;
    
    adjMatrix[3][4] = 1;
    adjMatrix[4][3] = 1;
    
    adjMatrix[3][6] = 2;
    adjMatrix[6][3] = 2;
    
    adjMatrix[4][5] = 2;
    adjMatrix[5][4] = 2;
    
    adjMatrix[4][6] = 1;
    adjMatrix[6][4] = 1;
    
    adjMatrix[5][6] = 2;
    adjMatrix[6][5] = 2;
    
    // Our adjacency matrix is complete.
    return adjMatrix;
    }
//////////////////////////////////////////////////////////////////////////////////////
    
// Given an Adjacency List, find all shortest paths from "start" to all other vertices.
vector< vector<int> > FloydWarshall(vector< vector<int> > &adjMatrix)
    {
    cout << "Called Floyd Warshall.\n";
    cout << "\nGetting the shortest path from all nodes to all other nodes.\n";
    
    // Initialize a solution matrix that's the same as the adjacency matrix.
    vector< vector<int> > dist;
    
    int n = adjMatrix.size();
    for(int i = 0; i < n; i++)
        {
        vector<int> row;
        dist.push_back(row);
        for(int j = 0; j < n; j++)
            {
            dist[i].push_back(adjMatrix[i][j]);
            }
        }
    
    // For each vertex w...
    for(int w = 0; w < n; w++)
        {
        // For each vertex as source (named u).
        for(int u = 0; u < n; u++)
            {
            // For each vertex as destination (named v).
            for(int v = 0; v < n; v++)
                {
                // If vertex w is on the shortest path from u to v...
                if(dist[u][w] + dist[w][v] < dist[u][v])
                    {
                    // Update value of dist[u][v]
                    dist[u][v] = dist[u][w] + dist[w][v];
                    }
                }
            }
        }
        
    return dist;
    }
    
void PrintShortestPath(vector< vector<int> > &dist)
    {
    cout << dist.size() << endl;
    cout << "\nPrinting the shortest paths for all nodes.\n";
    for(int i = 0; i < dist.size(); i++)
        {
        for(int j = 0; j < dist.size(); j++)
            {
            cout << "The distance from node " << i << " to node " << j << " is: " << dist[i][j] << endl;
            }
        cout << endl;
        }
    }
    
int main() 
    {
    cout << "Program started.\n";
    
    // Construct the adjacency matrix that represents our graph. 
    vector< vector<int> > adjMatrix = FormAdjMatrix();
    
    // Get a list of shortest path distances for all nodes.
    vector< vector<int> > dist = FloydWarshall(adjMatrix);
    
    // Print the list.
    PrintShortestPath(dist);
    
    cout << "Program ended.\n";
    
    return 0;
    }
The output for node 0 is the same as Dijkstra and Bellman-Ford. 

To Get The Path Itself

In our code, we saved the distance for each node from the source. But what if we need to know the actual shortest path (meaning what the nodes are, and not just the distance)?

Basically, in our distance list, we store not only the distance from "source node" to "current node", we also store the "previous node" in an int variable. 

​Here's some updated code to show Dijkstra's algorithm where paths are stored.
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161

// Copyright srcmake.com 2018.
// C++ Example Dijkstra Algorithm For Shortest Path (With PQ/Min-Heap)
// Official webpage for this tutorial: https://www.srcmake.com/home/cpp-shortest-path-dijkstra

/* The Dijkstra algorithm:
    // Initialize the graph adjacency list. adjList[i] = pair<int, int> where first is vertex, second is edge weight.
    // Initialize all source->vertex as infinite.
    // Create a PQ.
    // Add source to pq, where distance is 0.
    // While pq isn't empty...
        // Get min distance vertex from pq. (Call it u.)
        // Visit all of u's friends. For each one (called v)....
            // If the distance to v is shorter by going through u...
                // Update the distance of v.
                // Insert v into the pq. 
*/

// The example graph: https://www.srcmake.com/uploads/5/3/9/0/5390645/spgraph_orig.jpg

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// An adjacency list. Each adjList[i] holds a all the friends of node i.
// The first int is the vertex of the friend, the second int is the edge weight.
vector< vector<pair<int, int> > > FormAdjList()
    {
    // Our adjacency list.
    vector< vector<pair<int, int> > > adjList;
    
    // We have 7 vertices, so initialize 7 rows.
    const int n = 7;
    
    for(int i = 0; i < n; i++)
        {
        // Create a vector to represent a row, and add it to the adjList.
        vector<pair<int, int> > row;
        adjList.push_back(row);
        }
    
    
    // Now let's add our actual edges into the adjacency list.
    // See the picture here: https://www.srcmake.com/uploads/5/3/9/0/5390645/spadjlist_orig.jpg
    
    adjList[0].push_back(make_pair(1, 2));
    adjList[0].push_back(make_pair(2, 3));
    
    adjList[1].push_back(make_pair(0, 2));
    adjList[1].push_back(make_pair(5, 1));
    
    adjList[2].push_back(make_pair(0, 3));
    adjList[2].push_back(make_pair(5, 2));
    
    adjList[3].push_back(make_pair(1, 4));
    adjList[3].push_back(make_pair(4, 1));
    adjList[3].push_back(make_pair(6, 2));
    
    adjList[4].push_back(make_pair(3, 1));
    adjList[4].push_back(make_pair(5, 2));
    adjList[4].push_back(make_pair(6, 1));
    
    adjList[5].push_back(make_pair(1, 1));
    adjList[5].push_back(make_pair(2, 2));
    adjList[5].push_back(make_pair(4, 2));
    adjList[5].push_back(make_pair(6, 2));
    
    adjList[6].push_back(make_pair(3, 2));
    adjList[6].push_back(make_pair(4, 1));
    adjList[6].push_back(make_pair(5, 2));
    
    // Our graph is now represented as an adjacency list. Return it.
    return adjList;
    }
    
// Given an Adjacency List, find all shortest paths from "start" to all other vertices.
vector< pair<int, int> > DijkstraSP(vector< vector<pair<int, int> > > &adjList, int &start)
    {
    cout << "\nGetting the shortest path from " << start << " to all other nodes.\n";
    vector<pair<int, int> > dist; // First int is dist, second is the previous node. 
    
    // Initialize all source->vertex as infinite.
    int n = adjList.size();
    for(int i = 0; i < n; i++)
        {
        dist.push_back(make_pair(1000000007, i)); // Define "infinity" as necessary by constraints.
        }
        
    // Create a PQ.
    priority_queue<pair<int, int>, vector< pair<int, int> >, greater<pair<int, int> > > pq;
    
    // Add source to pq, where distance is 0.
    pq.push(make_pair(start, 0));
    dist[start] = make_pair(0, start);;
    
    // While pq isn't empty...
    while(pq.empty() == false)
        {
        // Get min distance vertex from pq. (Call it u.)
        int u = pq.top().first;
        pq.pop();
        
        // Visit all of u's friends. For each one (called v)....
        for(int i = 0; i < adjList[u].size(); i++)
            {
            int v = adjList[u][i].first;
            int weight = adjList[u][i].second;
            
            // If the distance to v is shorter by going through u...
            if(dist[v].first > dist[u].first + weight)
                {
                // Update the distance of v.
                dist[v].first = dist[u].first + weight;
                // Update the previous node of v.
                dist[v].second = u;
                // Insert v into the pq. 
                pq.push(make_pair(v, dist[v].first));
                }
            }
        }
    
    return dist;
    }
    
void PrintShortestPath(vector< pair<int, int> > &dist, int &start)
    {
    cout << "\nPrinting the shortest paths for node " << start << ".\n";
    for(int i = 0; i < dist.size(); i++)
        {
        cout << "The distance from node " << start << " to node " << i << " is: " << dist[i].first << endl;
        
        int currnode = i;
        cout << "The path is: " << currnode;
        while(currnode != start)
            {
            currnode = dist[currnode].second;
            cout << " <- " << currnode;
            }
        cout << endl << endl;
        }
    }
    
int main() 
    {
    cout << "Program started.\n";
    
    // Construct the adjacency list that represents our graph. 
    vector< vector<pair<int, int> > > adjList = FormAdjList();
    
    // Get a list of shortest path distances for node 0.
    int node = 0;
    vector< pair<int, int> > dist = DijkstraSP(adjList, node);
    
    // Print the list.
    PrintShortestPath(dist, node);
    
    cout << "Program ended.\n";
    
    return 0;
    }
The changes are to "vector<int> dist"" to "vector< pair<int, int> > dist" in our Dijkstra function (as well as line 116 where we store the previous node), the main function where the result is returned, and in the print function. 

Conclusion

It takes some time to understand shortest path algorithms, but with some practice, it becomes second nature.

Next up in the graphing algorithm series is the Ford-Fulkerson algorithm for Maximum Flow. Check out this bloc post to see it.
​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake
References
1. www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-using-priority_queue-stl/
2. www.geeksforgeeks.org/dynamic-programming-set-23-bellman-ford-algorithm/
​3. www.geeksforgeeks.org/dynamic-programming-set-16-floyd-warshall-algorithm/

Comments are closed.

    Author

    Hi, I'm srcmake. I play video games and develop software. 

    Pro-tip: Click the "DIRECTORY" button in the menu to find a list of blog posts.
    Metamask tip button
    License: All code and instructions are provided under the MIT License.

    Discord

    Chat with me.

    Youtube

    Watch my videos.

    Twitter

    Get the latest news.

    Twitch

    See the me code live.

    Github

    My latest projects.
Powered by Create your own unique website with customizable templates.