C++ Graph Connected Components and Cycles

Introduction: Connected Components and Cycles

In previous blog posts, we've gone over graph theory, adjacency lists, adjacency matrixes, and BFS/DFS. We had another blog post on shortest paths in a graph. We also looked at maximum flow using the Ford Fulkerson Algorithm. 

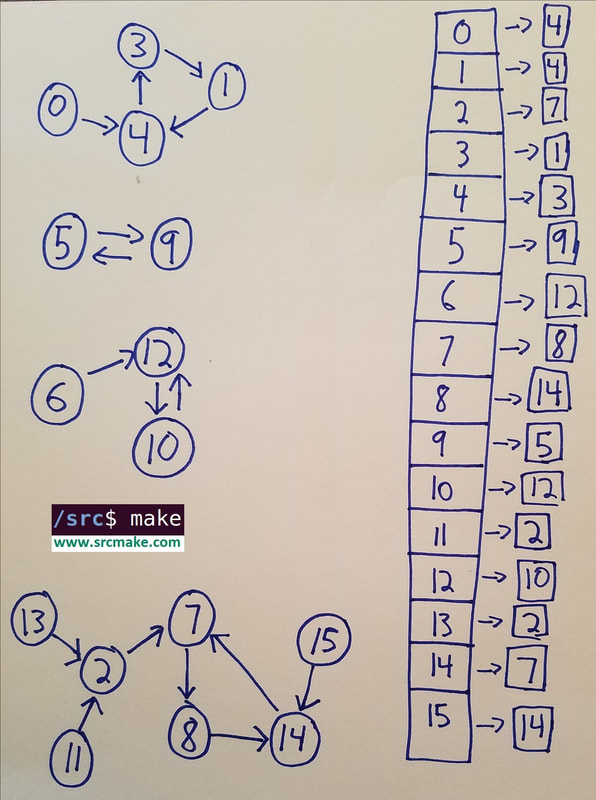
Today, we'll look at connected components and cycles in a graph. The graph that we'll be playing with is below. 

Connected Components

A graph has some vertices, named nodes. It also has some edges, that connect nodes. But that doesn't mean that all nodes are reachable from all other nodes, and that everything is connected nicely. For example, we could have 10 nodes, but only 1 edge. That's still a valid graph. 

A "connected component" is a set of vertices/edges that are connected. (The vertices can reach each other through edges.) 

In our code, we'll represent connected components by labeling them with a number. We'll create an array that, for each node in the graph (the node being represented by the index in the array), holds the number for the connected component the node is in.

To find out which connected component each node is in, we'll do a DFS and label each node as we see it.

Note: There's a special case where a node in a connected component does not get reached by other nodes, but is still part of a connected component. For example, node 15 in our group can go to node 14, but no other node can get to 15. We have to make sure that if a node can reach another node that's already part of a connected component, (Basically, someone shows up late to class, the class has people getting together to form groups for a project, but the guy's friend already got them both a group.) 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141

// Copyright srcmake 2018. // C++ Graph Connected Components. /* Algorithm: // 0. Read the graph into an adjacency list. // 1. Create an array for each node's component. Initialize it to -1. (This also acts as our "visited" array for DFS.) // 2. Create a counter variable (set to -1) for the number of component's we've seen. // 3. For each node in our graph... // 4. If this node's component is -1, then it hasn't been seen yet. So... // 5. Increment the counter by 1. // 6. Mark this node's component as counter. // 7. Perform DFS on this node, and mark all of it's neighbor's components as counter. // 8. If the neighbor of a vertex already is part of a group (connected component), then this node joins it too. */ // The example graph: https://www.srcmake.com/uploads/5/3/9/0/5390645/connectedcomponents_1_orig.jpg #include <iostream> #include <vector> using namespace std; ////////////////////////////////////////////////////////////////////////////////////////////// vector< vector<int> > FormAdjList() { vector< vector<int> > adjList; // We have 10 vertices, so initialize 10 rows. const int n = 16; for(int i = 0; i < n; i++) { // Create a vector to represent a row, and add it to the adjList. vector<int> row; adjList.push_back(row); } adjList[0].push_back(4); adjList[1].push_back(4); adjList[2].push_back(7); adjList[3].push_back(1); adjList[4].push_back(3); adjList[5].push_back(9); adjList[6].push_back(12); adjList[7].push_back(8); adjList[8].push_back(14); adjList[9].push_back(5); adjList[10].push_back(12); adjList[11].push_back(2); adjList[12].push_back(10); adjList[13].push_back(2); adjList[14].push_back(7); adjList[15].push_back(14); return adjList; } ////////////////////////////////////////////////////////////////////////////////////////////// /////////////////////////////////////////////////////////////////////////////////////////////// // Visit all nodes in a connected component. For each node seen, mark it with counter. int AdjListDFSComponents(vector< vector<int> > &adjList, int &vertex, int counter, vector<int> &componentArray) { // 6. Mark this node's component as counter. componentArray[vertex] = counter; // Is a neighbor already part of a group? // For example, node 15 is processed last, but it's part of a group since 14 is part of a group. int friendAlreadyGotThemAGroup = -1; // Look at this vertex's neighbors. for(int i = 0; i < adjList[vertex].size(); i++) { int neighbor = adjList[vertex][i]; // Recursively call DFS on the neighbor, if it wasn't visited. if(componentArray[neighbor] == -1) { AdjListDFSComponents(adjList, neighbor, counter, componentArray); } // If this neighbor is part of a group, then this vertex will join that group. if(componentArray[neighbor] != -1) { friendAlreadyGotThemAGroup = componentArray[neighbor]; } } // 8. If the neighbor of a vertex already is part of a group (connected component), then this node joins it too. if(friendAlreadyGotThemAGroup != -1) { componentArray[vertex] = friendAlreadyGotThemAGroup; } } ////////////////////////////////////////////////////////////////////////////////////////////// ////////////////////////////////////////////////////////////////////////////////////////////// int main() { cout << "Program started.\n"; // 0. Read the graph into an adjacency list. vector< vector<int> > adjList = FormAdjList(); int n = adjList.size(); // 1. Create an array for each node's component. Initialize it to -1. vector<int> componentArray; for(int i = 0; i < n; i++) { componentArray.push_back(-1); } // 2. Create a counter variable (set to -1) for the number of component's we've seen. int counter = -1; // 3. For each node in our graph... for(int i = 0; i < n; i++) { // 4. If this node's component is -1, then it hasn't been seen yet. So... if(componentArray[i] != -1) { continue; } // 5. Increment the counter by 1. counter += 1; // 7. Perform DFS on this node, and mark all of it's neighbor's components as counter. AdjListDFSComponents(adjList, i, counter, componentArray); } // Print the results. for(int i = 0; i < n; i++) { cout << "Node " << i << " belongs to component " << componentArray[i] << ".\n"; } cout << "Program ended.\n"; return 0; } //////////////////////////////////////////////////////////////////////////////////////////////

Cycles

A cycle in a graph happens if it's possible to travel along the edges on a graph where you can revisit a previous node. For example, in our graph above, someone on node 4 can get to node 3, and from node 3 they can get to node 1, and then from node 1 they can get back to node 4. That's a cycle. 

The code to find a cycle is pretty simple. It's just a DFS or BFS, and if we ever "visit" a node that's already been visited before, then we've detected a cycle. 

​Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels. 

Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
​Github: srcmake